How do I prove that equation of pair of tangents to a conic is $T^2=SS_0$?

Question

Let $$\textbf M=\begin{bmatrix}a & h & g \\ h & b & f \\ g & f & c\end{bmatrix} \qquad \textbf r=\begin{bmatrix}x \\ y \\ 1\end{bmatrix}\qquad \textbf{r}_k=\begin{bmatrix}x_k \\ y_k \\ 1\end{bmatrix}\qquad \mathrm d\textbf{r}=\begin{bmatrix}\mathrm dx \\ \mathrm dy \\ 0\end{bmatrix}$$ Then equation of conic is $\mathrm S \equiv\textbf{r}^{\mathrm T}\textbf{Mr}=0$

• Firstly, $\ \vec{\textbf a}^{\ \mathrm T}\textbf{M}\vec{\textbf b}=\vec{\textbf b}^{\ \mathrm T}\textbf{M}\vec{\textbf a}$

• Next, $\mathrm {dS}=2\textbf{r}^{\mathrm T}\textbf{M}\mathrm d\textbf r$

• Equation of tangent at $\textbf r_1$ is $\textbf{r}_1^{\mathrm T}\textbf{M}\textbf r=0$

• Equation of Chord of contact from $\textbf r_0$ is $\textbf{r}_0^{\mathrm T}\textbf{M}\textbf r=0$

My attempts for proving $\mathrm{T^2=SS_0}$ is the pair of tangents.

• The pair of tangents is $(\textbf{r}_1^{\mathrm T}\textbf{M}\textbf r)(\textbf{r}_2^{\mathrm T}\textbf{M}\textbf r)=0$

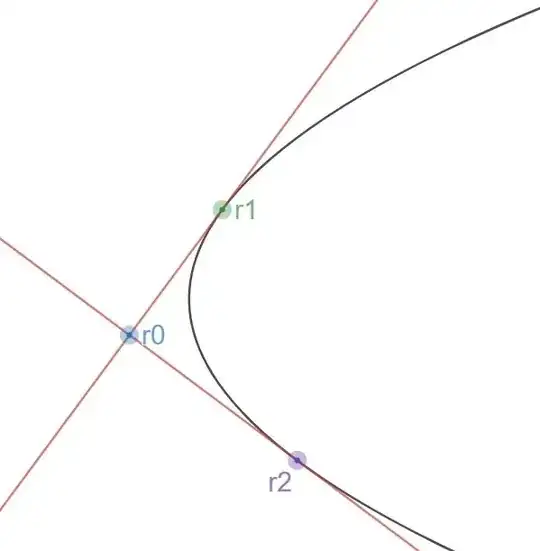
  • Sub Goal: to find a relation among $\textbf{r}_0$,$\textbf{r}_1$ and $\textbf{r}_2$

• The equation $(\textbf{r}_0^{\mathrm T}\textbf{M}\textbf r)^2-(\textbf{r}^{\mathrm T}\textbf{Mr})(\textbf{r}_0^{\mathrm T}\textbf{M}\textbf{r}_0)$ passes through $\textbf{r}_0$,$\textbf{r}_1$ and $\textbf{r}_2$. Thus if it is a degenerate hyperbola, then we are done.

  • Sub Goal: $\det(\textbf{M}\textbf{r}_0\textbf{r}_0^{\mathrm T}\textbf{M}-(\textbf{r}_0^{\mathrm T}\textbf{M}\textbf{r}_0)\textbf{M})=0$

• Assuming pair of tangents can be written as $\mathrm{T^2-\lambda S - \mu T}=0$. Now equating slopes at 1 and 2 reveals $\mu =0$ and and since it passes through 0, we get $\lambda=\mathrm S_0$

  • Sub Goal: proving the assumption.

Answer 1

To show that the matrix $\mathbf M\mathbf r_0\mathbf r_0^T\mathbf M-(\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M$ is singular it suffices to show that it has a nontrivial null space. The null space of a line consists of the points on the line, so the null space of a pair of lines consists of the points on both lines. We therefore expect that $\mathbf r_0$ is a null vector of the matrix, and indeed $$\begin{align} [\mathbf M\mathbf r_0\mathbf r_0^T\mathbf M-(\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M]\mathbf r_0 &= \mathbf M\mathbf r_0\mathbf r_0^T\mathbf M\mathbf r_0-(\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M\mathbf r_0 \\ &= (\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M\mathbf r_0-(\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M\mathbf r_0 \\ &= 0\end{align}.$$

This particular formulation of the tangent cone is related to the tangent-secant theorem. As well, it generalizes to higher dimensions: the tangent cone to a quadric $Q$ with vertex at $\mathbf v$ is $(Q\mathbf v)(Q\mathbf v)^T-(\mathbf v^TQ\mathbf v)Q$. (There’s another, and I think more straightforward, construction of the tangent cone in the plane, but it doesn’t generalize in the way this one does.)

This expression looks a lot like an application of Plücker’s mu to me, and sure enough it can be derived using that method. $\mathbf M\mathbf r_0$ is the polar line of $\mathbf r_0$, and so the degenerate conic $(\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)^T = \mathbf M\mathbf r_0\mathbf r_0^T\mathbf M$ is a double line that passes through the intersection points of of the conic $\mathbf M$ and the tangents through $\mathbf r_0$. Applying Plücker’s mu, a conic that shares these intersection points and also passes through $\mathbf r_0$ is $$\begin{align} (\mathbf r_0^T\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)^T-\mathbf r_0^T(\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)^T\mathbf r_0\mathbf M &= (\mathbf r_0^T\mathbf M\mathbf r_0)[(\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)^T - (\mathbf M\mathbf r_0)^T\mathbf r_0\mathbf M] \\ &= (\mathbf r_0^T\mathbf M\mathbf r_0)[(\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)^T - (\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M]. \end{align}$$ If $\mathbf r_0$ does not lie on the conic, we can drop the factor of $\mathbf r_0^T\mathbf M\mathbf r_0$ and have the required expression. If on the other hand $\mathbf r_0$ lies on $\mathbf M$, the tangent at that point is its polar line so we have the double line $(\mathbf M\mathbf r_0)(\mathbf M\mathbf r_0)^T$ from which we can freely subtract the term $(\mathbf r_0^T\mathbf M\mathbf r_0)\mathbf M$ since in this case $\mathbf r_0^T\mathbf M\mathbf r_0=0$.

Answer 2

I will use another formulation so I apologize beforehand.

Considering

$$ M =\left( \begin{array}{cc} a & b\\ b & c \end{array} \right), p = \left( \begin{array}{c} x\\ y\end{array} \right), p_0 = \left( \begin{array}{c} x_0\\ y_0\end{array} \right), p_1 = \left( \begin{array}{c} x_1\\ y_1\end{array} \right), \vec v = \left( \begin{array}{c} v_x\\ v_y\end{array} \right) $$

we have the conic $C$ and the line $L$

$$ \left\{ \begin{array}{rcl} C & \rightarrow & (p_1-p_0)\cdot M \cdot(p_1-p_0) = c_0\\ L & \rightarrow & p = p_1 + \lambda \vec v\\ \end{array} \right. $$

Now in $C \circ L = (p_1-p_0+\lambda \vec v) \cdot M\cdot (p_1-p_0+\lambda \vec v) = c_0$ tangency implies on

$$ \lambda^2\vec v \cdot M\cdot v +2\lambda (p_1-p_0)\cdot M\cdot \vec v +(p_1-p_0)\cdot M\cdot (p_1-p_0) = c_0 $$

$$ \Delta = (2(p_1-p_0)\cdot M\cdot \vec v))^2-4 (\vec v\cdot M\cdot\vec v)((p_1-p_0)\cdot M\cdot(p_1-p_0)-c_0) = 0 $$

From

$$ \lambda = \displaystyle{\frac{-2(p_1-p_0)\cdot M\cdot\vec v \pm \sqrt{\Delta}}{2\vec v\cdot M\cdot \vec v}} $$

Now simplifying $\Delta$ we get at the tangency condition in terms of $\vec v$

$$ \vec v\cdot(c_0 M-\det(M)(p_1-p_0)\cdot N \cdot (p_1-p_0))\cdot \vec v = 0 $$

with $N = \left(\begin{array}{c,c}1& -1 \\-1&1\\\end{array}\right)$ and $\sqrt{v_x^2+v_y^2} = 1$

hence giving $C$ and $p_1$ we can choose $\vec v$ for tangency.