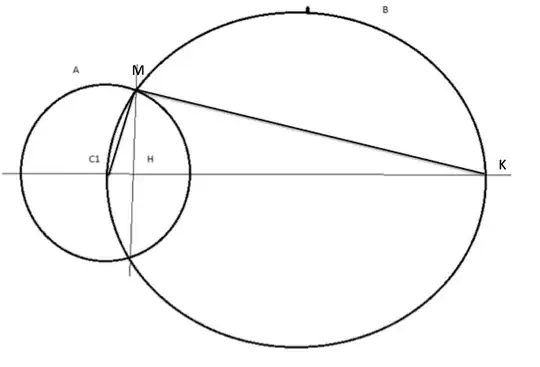
If have two circles intersecting along their diameter, let $A,B$ with radius $r_1, r_2$ in the ratio of $1:n/2$ (for $n$ being a positive real number), and overlapping area is the same as radius of smaller circle (let, $r_1$); then how to prove geometrically that the lune formed will be having the intersection point (shown as point $H$, on the line joining the diameters) with length from the center of the smaller circle as : $\frac{r_1}{n}$.
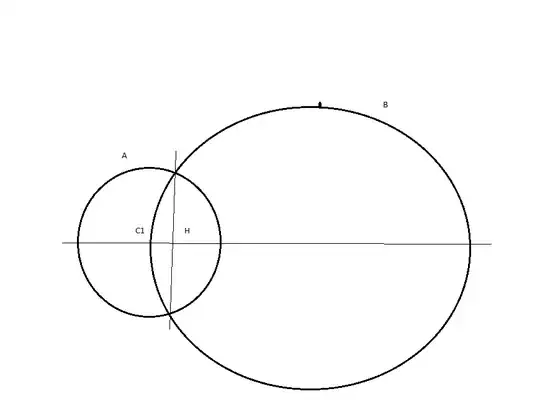
I can prove for different ratios of two circles individually and trying algebraically the two equations of different circles with diameters lying only on the $x$-axis.
Say, for ratio $n=5$, the two equations are given below with $b =r_1+2\cdot r_2$ being the total length of the two circles with intersecting length equal to $r_1$, assuming $r_1= \frac{b}{2^3}, r_2 = \frac{5r_1}{2}$ (or, diameter of circle $B=5r_1$) :
$$circle \,\,A :> (x-\frac{b}{8})^2 + y^2 = (\frac{b}{8})^2$$
$$circle \,\,B :> (x-\frac{7b}{16})^2 + y^2 = (\frac{5b}{16})^2$$
Have drawn at desmos too, the graph for the above at : https://www.desmos.com/calculator/e6dhp99eiu.
The graph also shows that the intersection point (shown by dotted line) is having length = $\frac{r_1}{5}$.
But a geometrical proof is needed.