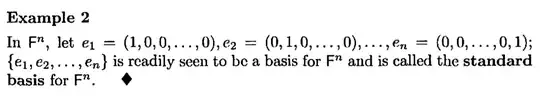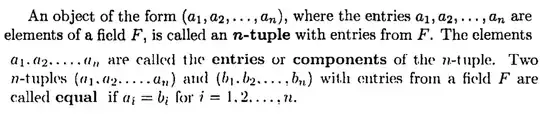0

I'm reading the definition of left-multiplication transformation, and it says ["]for each column vector $x\in\mathsf{F}^n$[."], but my original understanding is that each element of $\mathsf{F}^n$ is a tuple. I know in this definition it should be a column vector, or it will be a problem of how to place a tuple into column vector, i.e. vertically from top to bottom or bottom to top, to multiply it with a matrix. I'm confused about what's the actual meaning of $\mathsf{F}^n$. So is that

$$\textrm{["]Read a tuple left to right then it means the same thing of reading a column vector top-down[."]},$$

a convention?

Definition of left-multiplication transformation

And why I thought it could be a tuple can be traced back to another page of the same book

enter image description here

linear_combinatori_probabi
  • 1,551
  • 1
    Often in math the same name is used to refer to different, but closely related objects. So the name $F^n$ might sometimes refer to the set of all ordered $n$-tuples of elements of $F$, and might other times refer to the set of all $n \times 1$ matrices (that is, column vectors) with entries in $F$, even though these two sets are technically different. Hopefully the meaning is always clear from context. Usually I think of $F^n$ as the set of all $n \times 1$ column vectors with entries in $F$. – littleO Apr 15 '18 at 10:18
  • @IsanaYashiro which text book is the above excerpt from? – jII Nov 23 '18 at 21:25
  • @jesterII: Friedberg – linear_combinatori_probabi Nov 26 '18 at 09:12

3 Answers3

1

The advantage of vector $=$ column: the image of the vector by a linear function can be written as a matrix product.

Martín-Blas Pérez Pinilla
  • 41,546
  • 4
  • 46
  • 89
0

The way you write a vector, top-down or bottom-up as you say, doesn't play any role and shouldn't play of course. I would say that it makes our life easier to identify these two vector spaces and use interchangeably without any reference what is what. If you want to see it more mathematically, think the vector space with the vectors as tuples, and the other one as columns. Then there is clearly an obvious canonical isomorphism between these two $\mathbb{F}$-vector spaces. So we identify them.

0

After re-read all related definitions in my book, hopefully it's clear now:

  1. $\mathsf{F}^n$ is the set containing all n-tuple with entries from $F$.
  2. Of column vector or of row vector are just two different ways to represent/write down a given tuple. So No, it's by definition, not by convention.
  3. As the snapshot of the definitions, a column vector of a n-tuple is explicitly defined such that first component appear first, the second one is below the first one, and so on.

The concept of basis is not needed when describing column vector, since definition says all of it.

What's n-tuple
column/row vector as a representation of n-tuple

linear_combinatori_probabi
  • 1,551