What are different ways to compute $\int_{0}^{+\infty}\frac{\cos x}{a^2+x^2}dx$?

Question

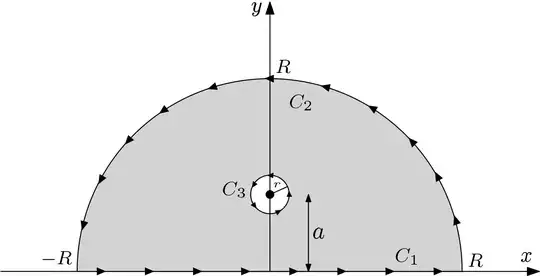
I am interested to compute the following integral

$$I=\int_{0}^{+\infty}\frac{\cos x}{a^2+x^2}dx$$

where $a\in\mathbb{R}^+$. Let me explain my first idea. As the integrand is an even function of $x$ then

$$2I=\int_{-\infty}^{+\infty}\frac{\cos x}{a^2+x^2}dx=\lim_{R\to+\infty}\int_{-R}^{R}\frac{\cos x}{a^2+x^2}dx:=\lim_{R\to+\infty}J$$

So, I first focus on computing the $J$ integral by first modifying it as follows

\begin{align*} J&=\int_{-R}^{R}\frac{\cos x}{a^2+x^2}dx=\int_{-R}^{R}\frac{\cos x}{a^2+x^2}dx+i\int_{-R}^{R}\frac{\sin x}{a^2+x^2}dx \\ &= \int_{-R}^{R}\frac{(\cos x+i\sin x)}{a^2+x^2}dx = \int_{-R}^{R}\frac{\exp(ix)}{a^2+x^2}dx \end{align*}

Then, I use the well-known techniques of complex variable theory. First, I replace the real variable $x$ in $J$ with a complex variable $z$ and consider a contour integral over $C=C_1\cup C_2$

$$K:=\int_{C}\frac{\exp(iz)}{a^2+z^2}dz$$

Then, according to the Cauchy's integral theorem and the Residue theorem, I get

\begin{align*} K=J+\int_{C_2}\frac{\exp(iz)}{a^2+z^2}dz &= \int_{C_3}\frac{\exp(iz)}{a^2+z^2}dz=\int_{C_3}\frac{\exp(iz)}{(z+ia)(z-ia)}dz \\ &=2\pi i \frac{\exp(i^2a)}{2ia}=\frac{\pi}{a}\exp(-a) \end{align*}

Next, taking the limit $R\to+\infty$ from the above relation, we obtain

$$2I+\lim_{R\to+\infty}\int_{C_2}\frac{\exp(iz)}{a^2+z^2}dz=\frac{\pi}{a}\exp(-a)$$

but, we can show that

$$\lim_{R\to+\infty}\int_{C_2}\frac{\exp(iz)}{a^2+z^2}dz=0$$

and then we can obtain the final result

$$I=\frac{\pi}{2a}\exp(-a)$$

First, please check my steps to see the final result is correct or not. Second, is there any other way to compute $I$?

Answer 1

For any $a>0$, $$ I(a)=\int_{0}^{+\infty}\frac{\cos(x)}{x^2+a^2}\,dx = \frac{1}{a}\int_{0}^{+\infty}\frac{\cos(ax)}{1+x^2}\,dx = \frac{J(a)}{a} $$ and the Laplace transform of $J(a)$ is given by $$ \int_{0}^{+\infty}J(a) e^{-sa}\,da = \int_{0}^{+\infty}\int_{0}^{+\infty}\frac{\cos(ax)e^{-sa}}{1+x^2}\,dx\,da $$ or, by invoking Fubini's theorem and integration by parts: $$ \int_{0}^{+\infty}\frac{s}{(1+x^2)(s^2+x^2)}\,dx =\frac{\pi}{2(1+s)}$$ by partial fraction decomposition. $\mathcal{L}^{-1}$ then gives $J(a)=\frac{\pi}{2}e^{-a}$ and $I(a)=\frac{\pi}{2a}e^{-a}$ as wanted.

Answer 2

A rather exotic approach leading to a known functional equation, which has an exponential solution.

Consider a function ($a>0$):

$$f(a)=a \int_{-\infty}^\infty \frac{\cos x}{a^2+x^2} dx=\int_{-\infty}^\infty \frac{\cos a x}{1+x^2} dx=\pi e^{-a}$$

Let's square it and change the dummy variable:

$$f^2(a)=\int_{-\infty}^\infty \int_{-\infty}^\infty \frac{\cos a x \cos a y}{(1+x^2)(1+y^2)} dx dy=$$

$$=\frac{1}{2} \int_{-\infty}^\infty \int_{-\infty}^\infty \frac{\cos a (x-y)+ \cos a (x+y)}{(1+x^2)(1+y^2)} dx dy$$

Due to the infinite limits, we can easily make substitutions in the form $x \pm y=t$, which will lead to the following expression under the integral:

$$\frac{\cos a t}{y^2+1} \left(\frac{1}{(y+t)^2+1} +\frac{1}{(y-t)^2+1} \right)$$

We will do partial fraction decomposition to integrate w.r.t. $y$.

$$\frac{1}{((y+t)^2+1)(y^2+1)}=\frac{1}{t (4+t^2)} \left(\frac{2y+3t}{(y+t)^2+1}-\frac{2y-t}{y^2+1} \right)$$

$$\frac{1}{((y-t)^2+1)(y^2+1)}=\frac{1}{t (4+t^2)} \left(\frac{-2y+3t}{(y-t)^2+1}-\frac{-2y-t}{y^2+1} \right)$$

---

Let's consider separately the 'problematic' integrals, but with finite limits:

$$\int_{-L}^L \frac{2y dy}{(y+t)^2+1}=\int_{-L-t}^{L+t} \frac{2u du}{u^2+1}-2t\int_{-L-t}^{L+t} \frac{du}{u^2+1} $$

The first integral vanishes, the second after taking the limit $L \to \infty$, gives us $-2 \pi t$. In the same way we find the other integral with $(y-t)^2$.

So the two 'problematic' integrals give us:

$$-2 \pi \int_{-\infty}^\infty \frac{\cos at ~dt}{4+t^2}$$

---

Grouping the other terms we get:

$$\frac{3t}{(y+t)^2+1}+\frac{3t}{(y-t)^2+1}+\frac{2t}{y^2+1}$$

After integration w.r.t. $y$ and adding all the results, we obtain:

$$f^2(a)=2\pi \int_{-\infty}^\infty \frac{\cos at ~dt}{4+t^2}=\pi f(2a)$$

The functional equation:

$$f^2 (a)=\pi f(2a)$$

has a general solution:

$$f(a)=\pi e^{c a}$$

We should have $c<0$, as can be seen by considering the original integral definition and taking the limit $a \to \infty$.

I'm not sure how to prove $c=-1$, but it should be possible.

Answer 3

Another way is to prove $$\int_\mathbb{R}\dfrac{a}{\pi}\dfrac{e^{ikx}}{a^2+x^2}=\exp -a|k|$$for $a>0$, by noting we're just trying to compute the characteristic function of a Cauchy distribution. The inversion theorem implies we need only check this characteristic function gives the right pdf. To prove $$\int_\mathbb{R}\exp (-ikx-a|k|)dk=\dfrac{2a}{a^2+x^2},$$write the left-hand side as the sum of integrals either side of $k=0$. The left-hand side is then $$\dfrac{1}{a+ix}+\dfrac{1}{a-ix},$$as required.