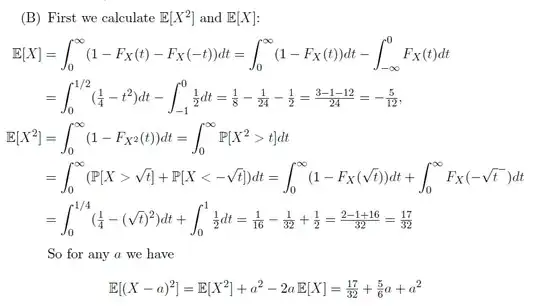If it is known that the random variable X has a CDF:
$$F_X(t)=\begin{cases} 0 && t\lt -1 \\ \frac{1}{2} && -1\le t \lt 0 \\ \frac{3}{4}+t^2 && 0\le t \lt \frac{1}{2} \\ 1 && \frac{1}{2} \le t \end{cases}$$
I wish to find $E[(X-a)^2]$ for all $a\in \mathbb R$
I found that $E[(X-a)^2]=E[X^2]-2aE[X]+a^2$
my teacher solved it this way:
what I'm trying to understand is the reason for the integrals used to find $E[X],E[X^2]$. Why does this work?
The first equality in the computation of $\mathbb E\left[X^2\right]$ follows from the fact that, for a non-negative random variable $Y$ with CDF $G$, we have that
$$ \mathbb E [Y]= \int_0^\infty y \,\mathrm d G(y) = \int_0^\infty (1-G(t))\,\mathrm d t. $$
You can find a proof of this here.
To see the first equality for $\mathbb E[X]$, we use the above result, along with the fact for a non-positive random variable $Y$ with CDF $G$,
$$ \mathbb E[Y] = \int_{-\infty}^0 y \,\mathrm d G(y) = -\int_{-\infty}^0 G(t) \, \mathrm d t. $$
You can prove this in a way similar to the analogous result for non-negative random variables.
Putting the two facts together allows us to write
\begin{align*} \mathbb E [X] &= \int_{-\infty}^\infty x \,\mathrm d F_X (x) \\ &= \int_0^\infty x\,\mathrm d F_X (x) +\int_{-\infty}^0 x \mathrm d F_X (x) \\ &= \int_0^\infty (1-F_X(t)) \,\mathrm d t - \int_{-\infty}^0 F_X(t)\,\mathrm d t. \end{align*}
