This is not a full answer, but may be useful for other users who are interested in this integral. Basically, we are getting back to the series, linked in the other question.
Let's try the series expansion valid for $|a|<1$:
$$\int_0^\infty \frac{e^{-x^2}}{1+a \cos x}dx=\sum_{n=0}^\infty (-1)^n a^n \int_0^\infty e^{-x^2} \cos^n x~dx$$
While I don't know any general expression for the integrals inside, using ' Lord Shark the Unknown's advice, we can certainly compute the first few terms, using:
$$\int_0^\infty e^{-x^2} \cos n x~dx=\frac{\sqrt{\pi}}{2} e^{-n^2/4}$$
See also Expand $\cos^n (x)$ in terms of $\cos{kx}$, $k=1,\dots,n$. which should help to find the general terms of the series (though it would be complicated).
For the first few terms we can explicitly write:
$$\cos^0 x=1 \\ \cos^1 x= \cos x \\ \cos^2 x=\frac{1}{2} (1+\cos 2x) \\ \cos^3 x=\frac{1}{4} (3 \cos x+\cos 3x) \\ \cos^4 x=\frac{1}{8} (3+4 \cos 2x+\cos 4x) \\ \cos^5 x=\frac{1}{16} (10 \cos x+5 \cos 3x+\cos 5x)$$
So we can bound the value of the integral (for $a>0$) by the partial sums:
$$S_4=\sum_{n=0}^4 (-1)^n a^n \int_0^\infty e^{-x^2} \cos^n x~dx$$
and:
$$S_5=\sum_{n=0}^5 (-1)^n a^n \int_0^\infty e^{-x^2} \cos^n x~dx$$
We have:
$$\int_0^\infty e^{-x^2} dx= \frac{\sqrt{\pi}}{2}\\ \int_0^\infty e^{-x^2} \cos x dx= \frac{\sqrt{\pi}}{2} e^{-1/4} \\ \frac{1}{2} \int_0^\infty e^{-x^2}(1+\cos 2x)dx=\frac{\sqrt{\pi}}{4} (1+e^{-1}) \\ \frac{1}{4} \int_0^\infty e^{-x^2}(3 \cos x+\cos 3x)dx=\frac{\sqrt{\pi}}{8} (3 e^{-1/4}+e^{-9/4}) \\ \frac{1}{8} \int_0^\infty e^{-x^2} (3+4 \cos 2x+\cos 4x) dx=\frac{\sqrt{\pi}}{16} (3+4 e^{-1}+e^{-4}) \\ \frac{1}{16} \int_0^\infty e^{-x^2} (10 \cos x+5 \cos 3x+\cos 5x) dx=\frac{\sqrt{\pi}}{32} (10 e^{-1/4}+5 e^{-9/4}+e^{-25/4})$$
We have:
$$S_5(a) < I(a) < S_4(a), \qquad 0<a<1$$
Here's the plot (scaled by $2/\sqrt{\pi}$ for convenience):
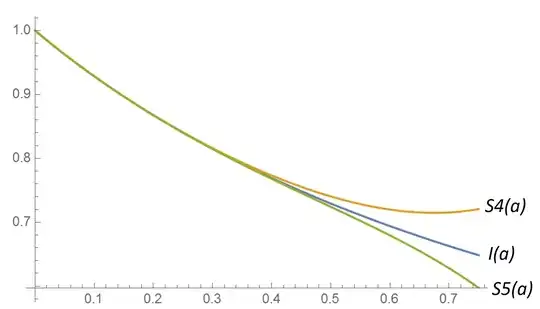
A much better approximation would be:
$$I(a) \approx \frac{S_4(a)+S_5(a)}{2}$$
which is a useful general trick for alternating series.
