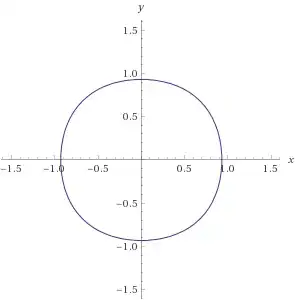
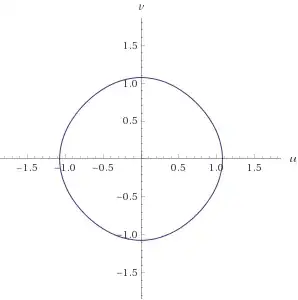
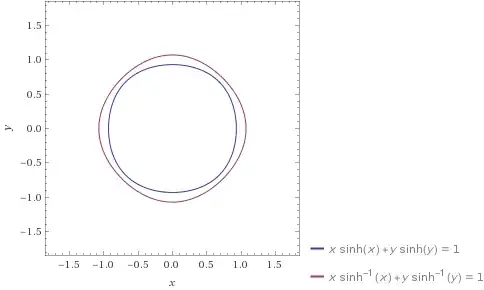
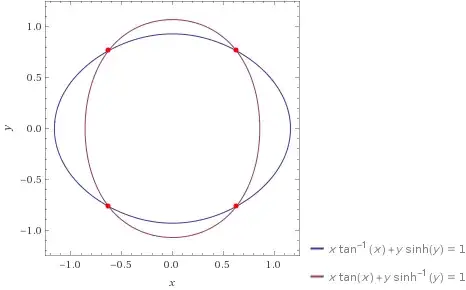
I am looking for a concrete example of a compact convex subset $K$ of $\mathbb{R}^2$ with $(0,0)$ center of symmetry, with a smooth boundary ( a $C^{\infty}$ $1$ dimensional submanifold of $\mathbb{R}^2$), such that its polar dual $K^{\circ}$ also has smooth boundary. Even better if both have analytic boundaries. Moreover, $K$ should not be an ellipse.
Comments: $K^{\circ}$, the convex dual is defined by $$K^{\circ} = \{ v \in \mathbb{R}^2\ | \ \langle v,u\rangle \le 1 \text{ for all } u \in K \}$$ (if we use $|\cdot |$ in the inequality we get the same thing).
It is easy to see that $K^{\circ}$ is compact, convex and symmetric. Moreover, it is a fact (duality theorem) that $K^{\circ \circ} = K$.
Examples: $K=\{(x,y)\ |\ \frac{x^2}{a^2} + \frac{y^2}{b^2}\le 1\}$. Then $K^{\circ} = \{(x,y)\ |\ a^2 x^2 + b^2 y^2\le 1\}$. In general, if $K=\{(x,y)\ |\ \frac{|x|^p}{a^p} + \frac{|y|^p}{b^p}\le 1\}$ then $K^{\circ} = \{(x,y)\ | \ a^q |x|^q + b^q |y|^q\le 1\}$ where $q$ is the Holder dual of $p$.
In the above example with $p$, $q$, we see that we cannot make both $K$,$K^{\circ}$ with boundary $C^{2}$, unless $p=q=2$.