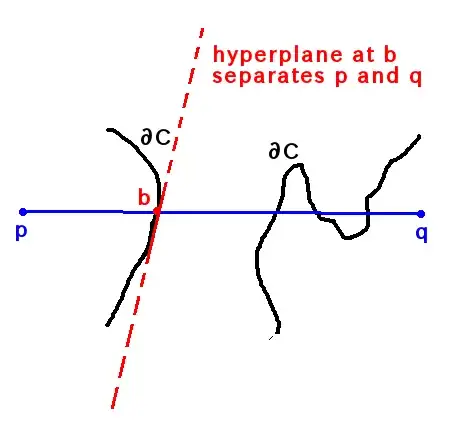
Exercise 2.27 in Boyd and Vanderberghe:
Suppose the set C is closed, has nonempty interior, and has a supporting hyperplane at every point in its boundary. Show that C is convex.
Seems to me one approach is to prove that the intersection of all the supporting hyperplanes is exactly C. Clearly this intersection contains C. Geometrically the other direction seems obvious, but any hint how to argue it rigorously?
Thanks!