Proving Area of circle by triangles

Question

I'm calculating with triangle to prove area of a circle. I start with a rectangle and I have 4 triangles in it. Area of a rectangle can be calculated by $ S = 4 (\frac12 r a) $ $$2r = a \Rightarrow r = \frac12 a $$ $$S = 4(\frac12ra) = 2ra = a^2$$

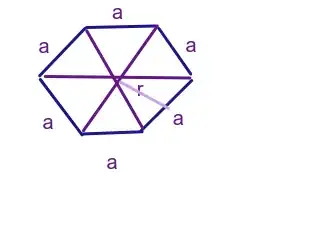
Area of Hexagonal is $ S = 6 (\frac12 r a) $

I name $n$ for triangles count $$S = n (\frac12 r a) $$ With adding triangles, the shape goes to be a circle:

Area of the circle is: $$S = \lim_{n\to ∞} \frac{n r a}{2} $$

How can I mathematically prove that: $$\lim_{n\to ∞} \frac{n r a}{2} = \pi r^2$$

Or if possible: $$\lim_{n\to ∞} \frac{n a}{2r} = \pi$$

In maths, try to use single alphabet for a single variable. I am referring to $fi$, you can call that $n$. — King Tut, Apr 05 '18 at 10:05
For your proof, use some geometry to deduce angles inside the regular polygons. Use trigonometry to get relations between side length and "$r$". — King Tut, Apr 05 '18 at 10:06

score 2 · Answer 1 · answered Apr 05 '18 at 10:11

In your proof, you need to use the angles subtended at the centre by the polygon. In general, $n$ sided polygon will subtend $\tfrac{2\pi}{n}$ at centre. And half of this angles is $\tfrac{\pi}{n}$. So we can say $\tan\tfrac{\pi}{n} = \tfrac{a}{2r}$. Substitute in your expression:

$$S = \lim_{n\to \infty} \frac{n r a}{2} = \lim_{n\to \infty} nr^2 \tan\tfrac{\pi}{n} = \pi r^2 $$

Sonal_sqrt · Accepted Answer · 2018-04-05T11:05:31.373

2

$$S=n(\frac12 ra)$$ If you are dividing the circle in $n$ triangles then angle at center of each triangle is $\frac{2\pi}n$. You know that the radius is $r$ of the circle then what is the base $a$. $$a=2r\sin\left(\frac{\pi}n\right)$$ Therefore $$S=n\left(r^2\sin\left(\frac{\pi}n\right)\right)$$ Take the limit of this and you get $$\lim_{n\rightarrow \infty}S=\pi r^2$$

An interesting observation.

Amir has taken the height of the triangle as $r$ and I have given a solution with hypoteneuse being $r$. Although both give the same limit they are different sequences. Amir's approach is such that the circle is contained inside the polygon and my approach is one where polygon is contained inside the circle. Which means the areas in Amir's case form an decreasing sequence and in my case form an increasing sequence.

edited Apr 05 '18 at 11:05

answered Apr 05 '18 at 10:11

Sonal_sqrt

4,711

If $r$ is as proposed by the images, you should use $\tan$ instead of $\sin$. As you take the limit, it does not matter for the end result :) – EdG Apr 05 '18 at 10:15
Yes i know. But it feels strange to take anything other than radius as $r$ in the circle. Anyway this serves as an alternate formulation. – Sonal_sqrt Apr 05 '18 at 10:18
@piyush in the limit of number of sides of polygon going infinity, we will have radius equal to radius of op. But still you raise a good point that it be better to reserve $r$ for radius! liked. – King Tut Apr 05 '18 at 10:33
I think you should use $tg$ instead of $sin$ – Amir Fo Apr 05 '18 at 10:45
I am not sure what is $tg$. – Sonal_sqrt Apr 05 '18 at 10:47
ops. I mean $tan$ – Amir Fo Apr 05 '18 at 10:50
Read my edit. It's a matter of convention. – Sonal_sqrt Apr 05 '18 at 11:06

score 1 · Answer 3 · answered Apr 05 '18 at 10:14

$r$ and $a$ in the proposed formula for the area of the hexagon are not free. The hexagon is uniquely parametrized by giving either $a$ or $r$. For the sake of this proof, $r$ is obviously the better choice since it is what we expect to occur in the end result. The area of the $n$-gon is then, with $n$ the number of triangles (instead of "$fi$"): $$S(n,r) = n S_\Delta(r,n)$$ and the area of a triangle with height $r$ and acute angle $2\pi/n$ is $$S_\Delta(r)=r^2\sin ( \pi/n )$$ For $n \to \infty$, we have $$\lim_{n\to\infty}S(n,r) = r^2 \lim_{m\to0} \frac {\sin(m)}m$$ which can be evaluated using L'Hôpital's rule to give $r^2 \pi$.

score 1 · Answer 4 · answered Apr 05 '18 at 10:14

1

If you have $f$ triangles, you will have an angle of $\theta = 2\pi /f$ at the center.

Now, consider $a$. You can easily show that

$$\frac{a}{2} = f\tan{\frac{\theta}{2}}$$

$$\frac{a}{2}=f\tan{\frac{\pi}{f}}$$

See if you can continue from here.

answered Apr 05 '18 at 10:14

Pritt Balagopal

1,115

Proving Area of circle by triangles

4 Answers4

Linked