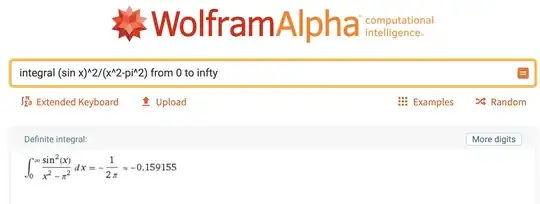
I will present a more elementary approach. First, note that if we expand the numerator at the singularity, first term in the Taylor series of the numerator $\sin^2{x}$ is $(x-\pi)^2$, and the denominator is $(x-\pi)(x+ \pi)$, so the singularity does not contribute to the integral (we can just remove the point $x = \pi$ from the region of integration), and we can treat it with elementary methods.
Short version (not very rigorous, as it involves substracting two diverging integrals from each other).
$$I = \int_0^\infty \frac{\sin^2{x}}{(x^2-\pi^2)} dx =\frac{1}{2} \int_{-\infty}^\infty \frac{\sin^2{x}}{(x^2-\pi^2)} dx \text{ (since even function)}$$
$$= \frac{1}{2} \int_{-\infty}^\infty \frac{\sin^2{x}}{(x-\pi)(x + \pi)} dx = \frac{1}{4\pi}\int_{-\infty}^\infty {\sin^2{x}}\left(\frac{1}{x-\pi} - \frac{1}{x+\pi}\right) dx $$
$$= \frac{1}{4\pi}\int_{-\infty}^\infty \frac{{\sin^2{x}}}{x-\pi} dx- \frac{1}{4\pi}\int_{-\infty}^\infty \frac{{\sin^2{x}}}{x+\pi}dx$$
Now substitute $(x - \pi) = t$ and $(x + \pi) = s$ in the two integrals.
Then the expression becomes $$\frac{1}{4\pi}\int_{-\infty}^\infty \frac{{\sin^2{(t + \pi)}}}{t} dt - \frac{1}{4\pi}\int_{-\infty}^\infty \frac{{\sin^2{(s-\pi)}}}{s} ds$$
$$= \frac{1}{4\pi}\int_{-\infty}^\infty \frac{{\sin^2{t}}}{t} dt - \frac{1}{4\pi}\int_{-\infty}^\infty \frac{{\sin^2{s}}}{s} ds = 0$$
In the last step, I substructed two diverging integrals from each other.
Long version (rigourous)
Let's first replace the upper limit with $N$, and we will consider $N \rightarrow \infty$ later.
$$I = \int_0^N \frac{\sin^2{x}}{(x^2-\pi^2)} dx =\frac{1}{2} \int_{-N}^N \frac{\sin^2{x}}{(x^2-\pi^2)} dx \text{ (since even function)}$$
$$= \frac{1}{2} \int_{-N}^N \frac{\sin^2{x}}{(x-\pi)(x + \pi)} dx = \frac{1}{4\pi}\int_{-N}^N {\sin^2{x}}\left(\frac{1}{x-\pi} - \frac{1}{x+\pi}\right) dx $$
$$= \frac{1}{4\pi}\int_{-N}^N \frac{{\sin^2{x}}}{x-\pi} dx- \frac{1}{4\pi}\int_{-N}^N \frac{{\sin^2{x}}}{x+\pi}dx$$
Now substitute $(x - \pi) = t$ and $(x + \pi) = s$ in the two integrals.
Then the expression becomes $$\frac{1}{4\pi}\int_{-N-\pi}^{N-\pi} \frac{{\sin^2{(t + \pi)}}}{t} dt - \frac{1}{4\pi}\int_{-N+\pi}^{N+\pi} \frac{{\sin^2{(s-\pi)}}}{s} ds$$
$$= \frac{1}{4\pi}\int_{-N-\pi}^{N-\pi} \frac{{\sin^2{t}}}{t} dt - \frac{1}{4\pi}\int_{-N+\pi}^{N+\pi} \frac{{\sin^2{s}}}{s} ds$$
$$= \frac{1}{4\pi}\int_{-N-\pi}^{-N+\pi} \frac{{\sin^2{t}}}{t} dt - \frac{1}{4\pi}\int_{N-\pi}^{N+\pi} \frac{{\sin^2{s}}}{s} ds$$
(the common term, $\frac{1}{4\pi}\int_{-N+\pi}^{N-\pi} \frac{{\sin^2{t}}}{t} dt$, cancels out)
Therefore,
$$|I| = \left|\frac{1}{4\pi}\int_{-N-\pi}^{-N+\pi} \frac{{\sin^2{t}}}{t} dt - \frac{1}{4\pi}\int_{N-\pi}^{N+\pi} \frac{{\sin^2{s}}}{s} ds \right| $$
$$ \leq \left|\frac{1}{4\pi}\int_{-N-\pi}^{-N+\pi} \frac{{\sin^2{t}}}{t} dt\right| + \left|\frac{1}{4\pi}\int_{N-\pi}^{N+\pi} \frac{{\sin^2{s}}}{s} ds \right| $$
$$ \leq \frac{1}{4\pi}\int_{-N-\pi}^{-N+\pi} \frac{1}{|t|} dt + \frac{1}{4\pi}\int_{N-\pi}^{N+\pi} \frac{1}{|s|} ds $$
$$ = \frac{1}{2\pi} \log{\frac{N+\pi}{N-\pi}} $$
$$ = \frac{1}{2\pi} \log{\left(\frac{1+\frac{\pi}{N}}{1-\frac{\pi}{N}}\right)}, $$
whose limiting value is $0$ as $N \rightarrow \infty$.
Therefore, $\lim_{N \rightarrow \infty} I = 0$.