Suppose we have 2 directional (not starting from the origin(0,0)) vectors u and v that are 2D vectors. Suppose (u and v) vectors can have any direction and can lie in any quadrant. The question is there a formula to find the angle between them?
Here is an image for more illustration:
After long search i found that i can use ATAN2() function for that, but the ATAN2() takes 2 positional vectors am i right?
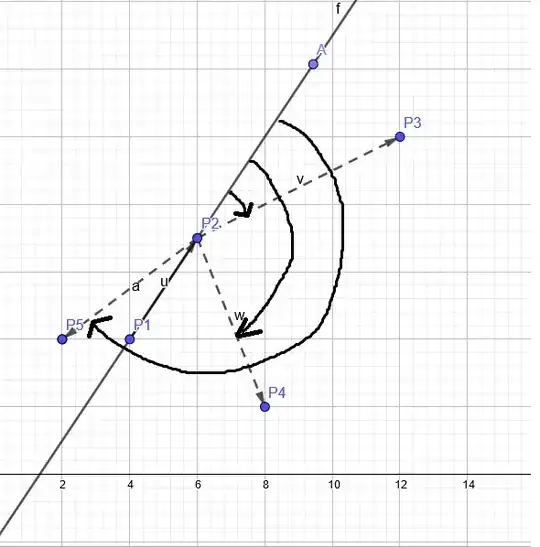
Suppose that $u = (x, y)$ and $v = (a, b)$.
Let $$ w = (-y, x) $$ and compute \begin{align} c &= v \cdot u \\ s &= v \cdot w \end{align} Then the angle from $u$ to $v$ is exactly $atan2(s, c)$.
Details: The "dot product" of two vectors $(p, q)$ and $(r, s)$ is $pr + qs$. The length $\| x \|$ of a vector $(p, q)$ is $\sqrt{p^2 + q^2}$. So the formulas for $c$ and $s$ become \begin{align} c &= ax + by\\ s &= -ay + bx. \end{align}
The only problem that can arise is that $c = s = 0$, in which case the value returned by atan2 will not be meaningful. This only happens when either $u$ or $v$ is the zero vector (or both are!), in which case the angle between them is undefined anyhow.
One last thing: you've asked for the angle measured CLOCKWISE, but my answer gives the angle measured COUNTERclockwise, because that's a really well-established standard in mathematics. If you want a clockwise angle, you'll need to negate the result that my formula gives you.
