1

Consider a family of lines $(4a + 3)x -(a+1)y -(2a+1) = 0$ where $a \in R$. The locus of the foot of the perpendicular from the origin of each member of this family is?

My Attempt:
Let the foot of the perpendicular from the origin on these lines be $(\alpha,\beta)$

Applying the formula of the foot of the perpendicular, I get
$$\alpha = \frac{8a^2 + 10a +3}{17a^2+26a+10}$$

$$\beta = -\biggl(\frac{2a^2+3a+1}{17a^2+26a+10}\biggr)$$

Now, I know that I need to eliminate '$a$' in order to get the locus. But, how am I supposed to do that? It's like quadratic on the top and bottom. Using the quadratic formula would be messy.

Any help would be appreciated.

Ski Mask
  • 1,910
Piano Land
  • 660

2 Answers2

1

One approach: write the two equations as polynomials in $a$ and compute their resultant. To wit, rewrite the equations $$x = {8a^2+10a+3 \over 17a^2+26a+10} \\ y = -{2a^2+3a+1 \over 17a^2+26a+10}$$ as $$(17a^2+26a+10)x-(8a^2+10a+3) = (17x-8)a^2+(26x-10)a+(10x-3) = 0 \\ (17a^2+26a+10)y +(2a^2+3a+1) = (17y+2)a^2+(26y+3)a+(10y+1) = 0.$$ Now form the Sylvester matrix of these two polynomials and compute its determinant (a symbolic algebra program is helpful here): $$\det\begin{bmatrix}17x-8&26x-10&10x-3&0 \\ 0&17x-8&26x-10&10x-3 \\ 17y+2&26y+3&10y+1&0 \\ 0&17y+2&26y+3&10y+1 \end{bmatrix} = 5(x^2-x+y^2-2y).$$ The resulting implicit Cartesian equation is therefore $$x^2+y^2-x-2y=0,$$ which is the equation of a circle of radius $\frac{\sqrt5}2$ centered at $\left(\frac12,1\right)$.

amd
  • 53,693
0

HINT.-Put $A=\dfrac{4a+3}{a+1}$ and $B=\dfrac{2a+1}{a+1}$ so you have to solve the system $$\begin{cases}y=Ax-B\\y=\dfrac{-x}{A}\end{cases}$$ so $$x =f(a)= {8a^2+10a+3 \over 17a^2+26a+10} \\ y =g(a)= -{2a^2+3a+1 \over 17a^2+26a+10}$$

This is a problem of difficult elimination (of the parameter $a$) that can be solved, as far as I know, only by the old Sylvester method as @amd has done. It is what I did to solve a problem once see at.

However, another way, patient but not intricate as in Silvester (in which it would be easy to make mistakes without using computers), could be as follows:

1) Calculate several points $(x, y)$ giving values to the parameter $a$.

2) With luck, the points obtained could configure the required curve.

3) In this case, the points obtained suggest a circumference.

4) Solve a system of three unknowns $h, k, r$ from $(x-h)^2+(y-k)^2=r^2$

We calculate eight points. $$\begin{array}{|c|c|}\hline a&-0.95&-0.9&-0.85&-0.8&-0.755&-0.75&-0.7&-0.5\\\hline f(a)&1.120622&1.297297&1.534246&1.5&0.168804&0&-0.615384&0\\\hline g(a)&0.070038&0.216216&0.575342&1.5&2.067852&2&0.923076&0\\\hline\end{array}$$

We have the following figure:

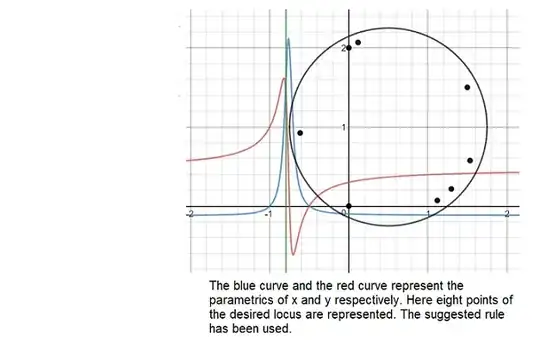
enter image description here

Important note here.- The black circle in the figure is the solution given by @amd and the non-drawn circle to which the points found belong are different, then one of the two answers is wrong. Probably mine although, even with a computer, one can make mistakes in the use of the Silvester method ....

Piquito
  • 29,594