0

Given a cubic bipartite planar graph. Its edges are 3-colored with black, blue and red. Let's define an orientation $R$ resp. $L$ at each vertex, when red, black and blue edges meet clockwise resp. anti-clockwise. The two examples of 3-edge-colored cubes shall demonstrate that this is easily done:

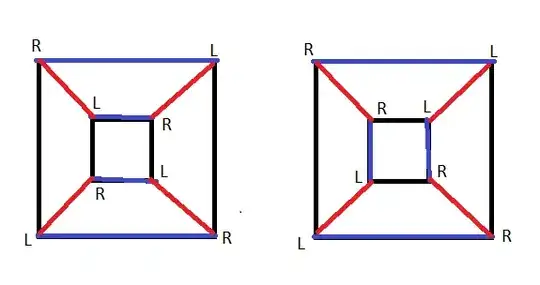
$\hskip2in$enter image description here

Is it conversely also possible to get a 3-edge-coloring, once a set of vertex orientations is given?

To be more concrete: I'm looking for a function $f$, that takes 1. an $n$-dimensional vector $\vec o$, containing the orientations of the $n$ vertices, and 2. the adjacency matrix $A$ of the given graph (and if necessary, 3. the original embedding $E$ of the vertices). $f$ returns three sets of colored edges, lets say as three subsets of $A$: $$ f(\vec o, A, E)=\{A_{black},A_{blue},A_{red}\} $$ In case that this is impossible, like for an all-$R$ orientation, $f$ shall return $\{\}$...

draks ...
  • 18,449
  • 1
    Consider some vertex, fixing one incident edge to one color forces which of the two other edges get what colors, and then further and further edges are implied too. Hence you can get potentially 3 colorings for each connected component. – dtldarek Mar 29 '18 at 20:40
  • @dtldarek Yes, I tried that for my example and it works. I wonder if this is still possible, when you're only given a list of orientations and the adjacency matrix...? I mean: no paint work! – draks ... Mar 29 '18 at 20:43
  • That will work if you have the graph and the original embedding (assuming you don't mind color permutations). If you have no embedding, then I don't know off the top of my head. – dtldarek Mar 29 '18 at 20:46
  • @dtldarek and how would this embedding look like? I mean in a linear algebar kind of way? – draks ... Mar 29 '18 at 20:53
  • The most straightforward way of encoding a planar embedding is just a map $\phi : V \to \mathbb{R}^2$, as in $\phi(v_{42}) = (123, 456)$ (and each vertex gets its own value). – dtldarek Mar 29 '18 at 21:24
  • @dtldarek lacking an embedding, is the problem equivalent hard as this one: Get the adjacency matrix of the dual of a 3-connected k -regular G without pen and paper? – draks ... Mar 30 '18 at 17:35
  • 1
    Whenever you know the orientation of a vertex and the color of one of the edges, the colors of its other two incident edges are given uniquely. Can't you just pick an edge at random, color it red, and continue with neighboring edges until you've covered everything? – hmakholm left over Monica Aug 05 '19 at 13:53
  • @HenningMakholm it looks too siple, but I can't find a counterexample... – draks ... Nov 28 '19 at 18:20

1 Answers1

1

Yes—you'll need an algorithm to compute it. Supposing your graph $G$ is connected, once you pick the color of one edge, the colors of all other edges are forced by the orientations of the vertices. Therefore, there are either exactly three ways to color the graph $G$ consistently (corresponding to cycling the colors $\text{red}\rightarrow\text{black}\rightarrow\text{blue}$) or it's altogether impossible.

Here's an algorithm to color your graph $G$. Make a new directed graph $H$. $H$ has one node for every edge in the original graph $G$, and $H$ has a directed edge $a\rightarrow b$ to mean "$a$ and $b$ are clockwise neighboring edges around an R vertex, or counterclockwise neighbors around an $L$ vertex." In other words, $a\rightarrow b$ means "If $a$ is colored red, then $b$ must be colored black."

Note that you can tell the relationship between the colors of two edges $a$ and $b$ by computing the path length between $a$ and $b$ in $H$: edges with the same color are connected purely by paths that are multiples of 3 in length. Edges with red/black black/blue blue/red relationships are connected purely by paths of length $3k+1$. And edges with red/blue, black/red, blue/black relationships are connected purely by paths of length $3k+2$.

Moreover, because $G$ is cubic, whenever edges are connected by a path of length $p$, they are connected by another path of length $p+3$. And if edges are connected, we can be sure that they are connected by a path of length at most $E$ (the number of edges in the graph).

Thus the coloring procedure is: Given a connected graph $G$ with $E$ edges, build the directed graph $H$ as an adjacency matrix, and let $u$ be a vector with 1 in some position and zeroes everywhere else. ($u$ represents a node in $H$, i.e. an arbitrary edge in $G$). Compute $\mathsf{RED}=H^{E}u$. Every nonzero entry in $\mathsf{RED}$ is an edge that should be colored red. Similarly, nonzero entries in $\mathsf{BLACK}=H^{E+1}u$ should be colored black, and nonzero entries in $\mathsf{BLUE}=H^{E+2}u$ should be colored blue. The problem is solvable if and only if every edge appears in exactly one of these three lists.

user326210
  • 17,287
  • Looks like you don't need information about embeddings? – draks ... Apr 13 '18 at 17:49
  • I do need information about the embedding, so I can know whether the edge is spatially counter/clockwise from its neighbor. It might be very possible to perform this algorithm while simultaneously incrementally generating an embedding, using the L/R constraints to rule out certain incompatible embeddings. – user326210 Apr 13 '18 at 18:03