3

I'm a Grade 12 student. The other day I was messing around with functions on my calculator and I came across $x^{2/3}$. When I evaluated a negative integer as x (using the memory function on my calculator) I was received with a domain error.

I asked my teacher about it and she said it was a fault in the calculator. I took this a bit further and put $(-64)^{2/3}$ into Wolfram Alpha/Google was some weird number like:

-8 +13.8564... i

Can someone explain to me why this does not evaluate to just 8? Using exponent laws that I learned this is equivalent to $\sqrt[3]{-64}^2=(-4)^2=16$.

(By the way I haven't learned about imaginary numbers yet)

David Liao
  • 143

3 Answers3

2

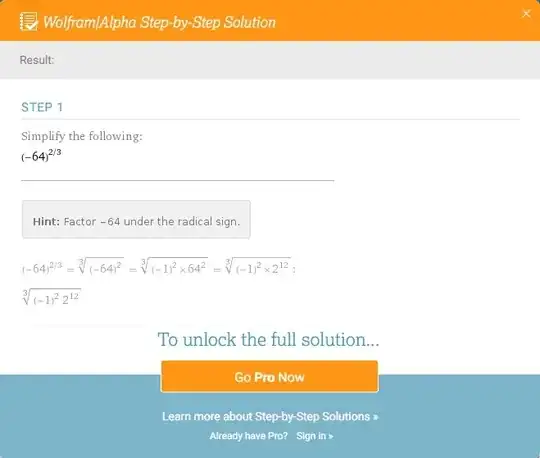
From school you surely know, that the equation $x^1 = 1$ has one $x^2 = 1$ has two solution. However, what about the equation $x^n = 1$?

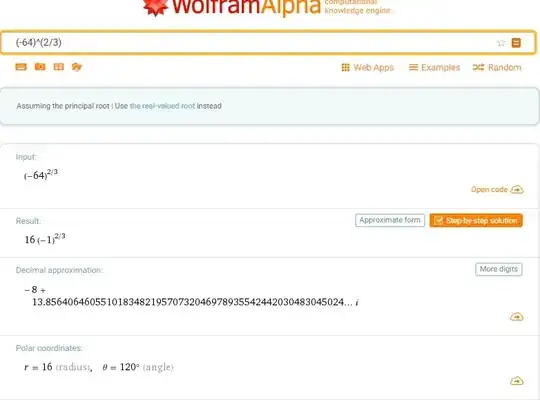
From school you know that this equation $x^n = 1$ would only have one or two solutions, depending on whether $n$ is even or odd. But wouldn't it be more interesting to have numbers that would give exactly n solutions? Well yes, there are such numbers, called complex numbers. In fact the number $-8 +13.8564...i$ you got is such a number, consisting of two parts: $-8$ is called the real part, $+13.8564...$i the imaginary part, one of the three solutions to the equation $${(x^\frac{1}{3}})^2 = x^\frac{2}{3} = {(x^2)}^{\frac{1}{3}} =-64$$

If you take above number, put it to the power of $3$, you will get again $-64$. (On a side note: Maybe the number can not be represented exactly, so it is possible you get again a complex number, however that number is sure to have a real part very close to $-64$ and an imaginary part extremely close to $0$.)

I recommend you play a bit around in wolfram alpha with the equation $x^n = 1$, just pluck in some numbers for $n$. What can you say about the roots of this equation? Where do they lie in the complex plane? (Imagine the plane to be just your normal, usual coordinate system from school. Instead of the $x-y$ however you now just label the axis $x$ and $i$..)

If you connect two neighbored roots, what is their distance from each other, what about the angle between three of such roots? I am pretty sure you will find some interesting results. (A glimpse of a lot more to come...)

Imago
  • 2,132
1

Two obvious definitions of $x^{2/3}$ you could try for $x\in\mathbb{R}$ are $\sqrt[3]{x^2}$ and $(\sqrt[3]{x})^2$, and in both cases the $-$ sign has no effect. For example, $$\sqrt[3]{(\pm 64)^2}=\sqrt[3]{4096}=16=(\pm 4)^2=(\sqrt[3]{\pm 64})^2.$$Software that gives you any other answer is "overthinking it". It's due to the way complex numbers work, specifically a concept called roots of unity. I realise that concept might be a bit advanced for this, but I'll give a brief overview. In the particular example you cite, the number $-64=-64+0i$ can be obtained by rotating the positive number $64$ through an angle of $\pi$ radians in the complex plane, and the two-thirds power is obtained by rotating $64^{2/3}=16$ through an angle of $2\pi/3$, multiplying it by $\frac{-1+i\sqrt{3}}{2}$.

J.G.
  • 115,835
0

For your interest, here is the step-by-step screenshot (trial version only):enter image description here

This happens because you are using the principal root feature. Here is another screenshot:

enter image description here

Click on "Use the real-valued root instead" will give you the correct solution as calculated.

On my CASIO calculator, the correct result is also $16$.

user061703
  • 3,877