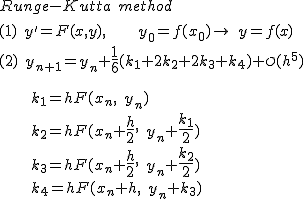2

I felt I had some sort of intuition for the Runge-Kutta method up to second order, but for the fourth order I have some confusions. Also, my idea of it could be totally wrong in the first place.

So, I'll just repeat it here:

$$y_n = y_{n-1} + (1/2)(k_1+k_2)$$

Where

$$k_1=hf(x_{n-1},y_{n-1})$$ $$k_2=hf(x_{n-1}+h,y_{n-1}+k_1)$$

Now the way I try and rationalize it is this:

  • $k_1$ is the change in $y$ for the forward Euler method
  • $k_2$ looks like an Euler step but with a step forward in $x$, with $h$, and a step forward in $y$, $k_1$, in accordance with the step in $x$. It seems sort of like a a slope for the next point, for $y_n+1$)
  • The next point $y_n$ is the average of those two $k$ values, which are slopes.

I don't think I have this right, as, to my logic, $k_2$ should be the increment from $y_n$ to $y_{n+1}$.

Now, for the fourth order method, it looks like this (and I'm lazy so I'll just attach an image instead of writing it all up):

enter image description here

Here, I think my intuition falls apart, as I cannot explain, for instance, why $k_2$ and $k_3$ are using $h/2$ and $k/2$ increment increases while $k_1$ and $k_4$ do not.

However, it looks like an average again.

Can someone help illuminate this for me?

sangstar
  • 1,947

1 Answers1

2

I studied it a long time ago, so take my answer with a grain of salt.

The intuition behind Runge-Kutta schemes is approximating the solution $x(t)$ of $\dot{x}=f(t,x)$ by a weighted mean of some intermediate values of $f(t,x)$, calculated at some points in the interval $[t,t+h]$. Thus, we calculate $f$ at, say, $t+\frac{h}{2}$ , use it to estimate $x(t+\frac{h}{2})$, and use this new $x$ to refine the calculation of $f$, and then average all those estimations.

Those seemingly strange coefficients come from the derivation of the method. I won't write the calculations, but only give the general idea behind how to derive a general explicit Runge-Kutta scheme. If you write down in mathematical language how the method should work, it takes this form:

$$x_{n+1}=x_n+h\sum_{i=1}^m \alpha_ik_i$$

where $k_i = f(t+\beta_ih, x_n+\gamma_ik_{i-1})$.

You want a method that works to a precision of $O(h^5)$. Thus, you expand $x_n=x(t+h)$ as a Taylor series up to the $h^5$ term, and note that the $n^{th}$ derivatives are actually $(n-1)^{th}$ derivatives of $f$. Also, when you expand those $k_i$ as Taylor series around $f(t,x_n)$ up to $O(h^5)$, you'll see the same derivatives appearing, but with coefficients.

Plugging in the results of the expansion of $x_{n+1}$ in the left-hand side, and the results from all $k_i$ in the right-hand side, you will be able to compare the coefficients of the powers of $h$ which will give you a system of equations. If I recall correctly, this system will have more unknowns than equations, so you'll have freedom to pick some values for a few of them. I don't remember now the exact conditions to arrive at the usual RK4 scheme, but this shouldn't be hard to find.

AspiringMathematician
  • 2,218
  • 12
  • 28