1

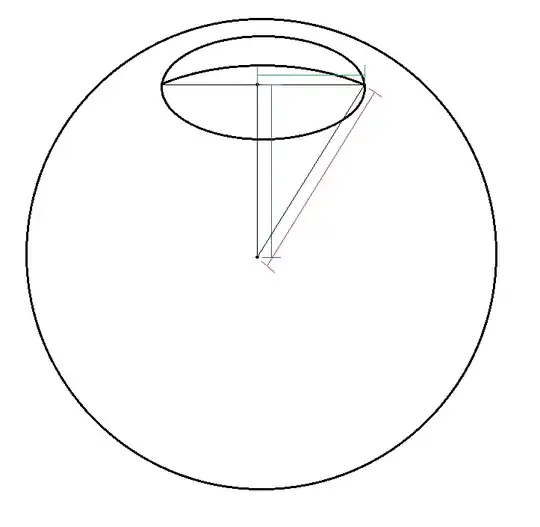
How can I find the radius of a sphere if I am given the radius of an intersecting circle- 24cm. The only other unit I am given is the distance from the center of the circle to the top- most point of the sphere- 32cm. How would I go about solving this problem.

Nandha
  • 11

2 Answers2

1

In the picture below, you are given that the length in green is $24$ cm and that the length in blue is $32$ cm. You want to calculate the length in red which is the hypotenuse of the triangle with sides $24$ cm and $32$ cm. So the length in red is equal to $(24^2+32^2)^{1/2}=40$ cm.

enter image description here

mzp
  • 1,925
  • 2
  • 18
  • 41
  • Thanks for the help, but what is to say that hypotenuse is the radius of the sphere, there is nothing saying the intersecting circle is the midpoint. – Nandha Mar 28 '18 at 16:52
  • The hypotenuse starts at the center of the sphere and ends at a point in which the circle is intersecting the sphere which must be part of the boundary of the sphere. Therefore, it is the radios of the sphere. – mzp Mar 28 '18 at 18:55
0

The equation of a sphere can be given by $$x^2+y^2=r^2-z^2$$ where $r^2-z^2$ is the square of radius of any intersecting circle at height $z$ from center of sphere Hence $$r^2-z^2=24^2$$ and $r-z=32$. Solving simultaneously \begin{align} r&=25 \text{ cm (radius of sphere)} \\ z&=-7 \text{ cm} \end{align}

Xander Henderson
  • 29,772
Mohammed
  • 1