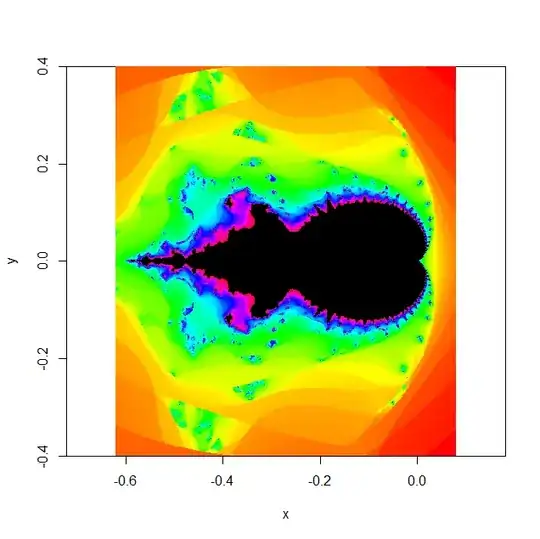
The Mandelbrot and Julia type fractals are very Well known.
But such fractals follow from
$$z_n = f(z_{n-1},c)$$
In other words a recursion that only depends on the previous value and a constant. ( you could argue the starting value too , but it has “ No memory “ )
What would happen If we consider recursions based on the 2 last values ??
Would the shapes be similar looking fractals ? Different looking fractals ? Not fractals ?? More like a cellular automaton ??
For instance
We start with complex $z$ as first value. Second is $z/2$.
Then
$$ z_{n+2} = z_{n+1}^2 + z_n^2 + c$$
How would that look like ??