3

Here's how my book derives the formula for the volume of the sphere:

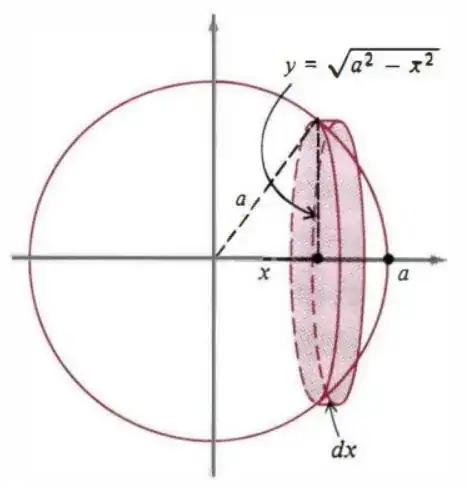
A sphere can be thought of as the solid of revolution generated by revolving a semicircle about its diameter (see the figure below). If the equation of the semi-circle is $x^2+y^2=a^2$, then the element of volume is $dV=\pi y^2dx=\pi(a^2-x^2)dx$ and the volume of the sphere is given by $$V=2\int_0^a{\pi(a^2-x^2)dx}=\frac{4}{3}\pi a^3$$

So I thought: well, I know that the 'lateral' surface area of the element of volume $dV$ is just the circumference times a little change in $x$, so by the same reasoning the area of the sphere should be given by

$$2\int_0^a{2\pi\sqrt{a^2-x^2}dx}$$

That way we should be able to cover the whole surface of the sphere. Sure, there would still be an extra "peeling" around the outside of the strip, but as the book says, just as in the calculation of the volume, "this slight apparent error - due to using disks instead of actual slices - disappears as a consequence of the limit process that is part of the meaning of the integral sign.".

It turns out, however, that that integral does not equal $4\pi a^2$. So, what is wrong with my reasoning? Thanks in advance.

enter image description here

Sasaki
  • 1,199
  • 9
  • 16
  • You need to be sure that the “slight apparent error” really does disappear when you do this sort of thing. – amd Mar 26 '18 at 23:28
  • The answer to this question, which you can find in the list of related questions at right and is also a duplicate, is instructive. – amd Mar 26 '18 at 23:35

4 Answers4

5

You need to integrate the slanted area (thin slice of a cone) that bounds what you can think of as a thin cylinder when computing volume. It's longer than $dx$.

It's the same paradox that occurs when you try to calculate the length of a slanted line or the circumference of a circle by approximating it with a staircase of small steps.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
  • That makes sense to me, but why is it ok to use thin cylinders in the calculation of the volume of the sphere? I saw the other link with essentially the same question as mine, and one answer said that we can't approximate curves with horizontal lines. But isn't that basically what we're doing when we evaluate the area under a parabola, for instance, via integration? Thanks. – Sasaki Mar 27 '18 at 00:03
  • 2
    Good question. As another answer or comment suggests, you have to do a careful analysis of the error. In two dimensions (rather than three) you see that when you approximate a curve by a step function the error in the area decreases as the steps shrink (which is why Riemann sums converge to the integral) while the error in the arc length doesn't. – Ethan Bolker Mar 27 '18 at 00:23
1

It is the right idea, but the bands are slices of the frustum of a cone.

enter image description here

You need a factor of the slant height to $dx$

That factor is $\sqrt {1+\frac {dr}{dx}^2}$

$A = 2\pi\int r\sqrt {1+\frac {dr}{dx}^2} \ dx$

Or if your slices run horizonatally

$A = 2\pi\int r\sqrt {1+\frac {dr}{dy}^2} \ dy$

If $r = \sqrt {R^2-x^2}$

$\frac {dr}{dx} = -\frac {x}{\sqrt {R^2-x^2}}\\ y\sqrt {1+\frac {dr}{dx}^2} = \sqrt{R^2-x^2}\sqrt {1+\frac {x^2}{R^2-x^2}} = R$

$A = 2\pi \int_{-R}^R R \ dx = 4\pi R^2$

Doug M
  • 57,877
1

As you notice in your graph, the horizontal $dx $ does not take into account the slope of the sphere at the point $(x,y)$.

In order to count for the slope, you replace your $dx$ with the better estimate $$ds = \sqrt {1+(dy/dx)^2}dx$$

Mohammad Riazi-Kermani
  • 68,728
0

Your set up

$$2\int_0^a{2\pi\sqrt{a^2-x^2}dx}$$

is not valid for the surface of the sphere since we should consider $\frac{dx}{\sin \theta}=\frac{dx}{ \frac{ \sqrt{a^2-x^2}} {a} }=\frac{a}{\sqrt{a^2-x^2}}dx$, then

$$S=2\int_0^a{2\pi a\,dx}=4\pi a^2$$

user
  • 154,566