I just want to complete Hans Engler's answer. He already showed
$$x = -\frac 1\alpha -W\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)$$
$\alpha > 0$ implies $-\tfrac 1\alpha \in \mathbb{R}^{-}$ and thus $-\tfrac 1\alpha e^{-\tfrac 1\alpha} \in \left[-\tfrac 1e,0\right)$ (The function $z\mapsto ze^z$ maps $\mathbb{R}^-$ to $\left[-\tfrac 1e,0\right)$) The Lambert $W$ function has two branches $W_0$ and $W_{-1}$ on the interval $\left[-\tfrac 1e,0\right)$:
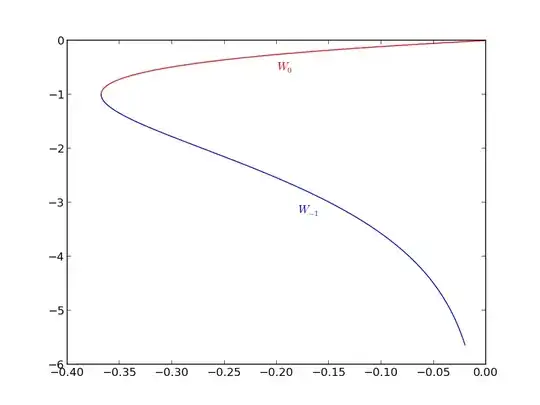
So we have the two solutions
$$x_1 = -\frac 1\alpha -W_0\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)$$
$$x_2 = -\frac 1\alpha -W_{-1}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)$$
One of $W_0\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)$ and $W_{-1}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)$ will always be $-\tfrac 1\alpha$ as $W$ is the inverse of the function $z \mapsto ze^z$. This solution of $W$ would give $x=0$ which must be canceled out for $\alpha \ne 1$ as $\phi(x)=1$ just for $x=0$.
Case $\alpha=1$: For $\alpha=1$ is $-\tfrac 1\alpha e^{-\tfrac 1\alpha}=-\tfrac 1e$ and thus $W_0\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)=W_{-1}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)=-1$. This gives $\phi^{-1}(1)=0$ as expected.
Case $\alpha > 1$: $\alpha > 1 \Rightarrow 0 < \tfrac 1 \alpha < 1 \Rightarrow -1 < -\tfrac 1 \alpha < 0$.
Because $W_0(y) \ge -1$ it must be $W_0\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)=-\tfrac 1\alpha$ and so
$$\phi^{-1}(\alpha) = -\frac 1\alpha -W_{-1}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)\text{ for } \alpha > 1$$
Case $\alpha < 1$: $0 < \alpha < 1 \Rightarrow \tfrac 1 \alpha > 1 \Rightarrow -\tfrac 1\alpha < -1$
Because $W_{-1}(y) \le -1$ we have $W_{-1}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)=-\tfrac 1\alpha$ and thus
$$\phi^{-1}(\alpha) = -\frac 1\alpha -W_{0}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right)\text{ for } \alpha < 1$$
Solution
The solution is
$$\phi^{-1}(\alpha) = \begin{cases} -\frac 1\alpha -W_{-1}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right) & ; \alpha > 1 \\ 0 & ; \alpha = 1 \\-\frac 1\alpha -W_{0}\left(-\frac 1\alpha e^{-\tfrac 1\alpha}\right) & ; \alpha < 1 \end{cases}$$