Last 4 digits using numeric systems

Question

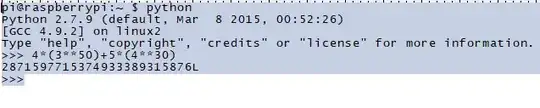
I have to find the last 4 digits of the number $4*(3^{50}) + 5*(4^{30})$ . The problem is part of a set of applications of numeral systems, so I thought that perhaps i could try to write it as $\,(10^0)*a + (10^1)*b + (10^3)*c$ and so on, but i don't know how to start. Any ideas?

Answer 1

Couldn't copy and paste text, so here's an image.

Answer 2

Last four digits $\pmod{10^4}$

As $3^2=10-1,$

$$3^{50}$$ $$=(10-1)^{25}=(-1+10)^{25}\equiv-1+\binom{25}110-\binom{25}210^2+\binom{25}310^3\pmod{10^4}$$ $$\equiv250-1$$

as $\binom{25}2\equiv0\pmod{10^2},\binom{25}3\equiv0\pmod{10}$

Again, $4^{30}=2^{60}$

Now $(5\cdot2^{60},10^4)=5\cdot2^4,$

like How to find last two digits of $2^{2016}$,

let us find $\dfrac{5\cdot2^4}{5\cdot2^{60}}\pmod{\dfrac{10^4}{5\cdot2^4}},$

i.e., $2^{56}\pmod{125},$

Now $2^7\equiv3\pmod{125}\implies2^{56}\equiv3^8\equiv3^5\cdot3^3\equiv-7\cdot27\equiv61$

$\implies5\cdot2^{60}\equiv61\cdot5\cdot2^4\pmod{10^4}$