2

I don't know if I understand correctly. The base situation is explained in the following image: 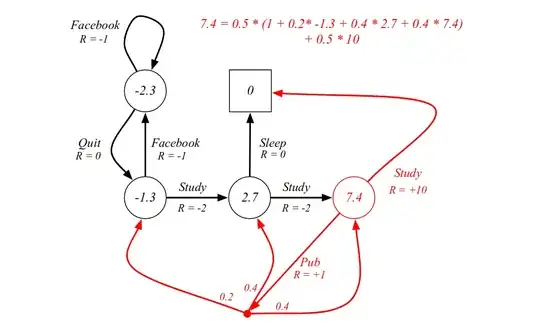https://i.stack.imgur.com/weFfw.png

formula: $s$ = state, $a$ = action, $A$ = set of actions, $S$ = set of states, $s'$ = next state, $P_{ss'}^a$ matrix of probabilities.

$$V_{\pi}(s) = \sum_{a \in A}\pi(a|s)(R_{s}^a + y\sum_{s' \in S}P_{ss'}^aV_{\pi}(s'))$$

My problem is that when I calculate the $V_{\pi(s)}$ for the state that has the action Pub. Because for the $V_{\pi(s)}$ I need to calculate all $V_{\pi(s')}$ and one of the $s'$ is the current $s$, I enter a loop.

My question are:

When I start the calculation are all state values null or is there some type of initial value?

If there are initial values, how can I calculate them?

Is my interpretation correct? Is there a loop or not?

If there isn't, can you explain why?

Thanks in advance for your answers.

Fabio Somenzi
  • 7,676
Michel Basili
  • 21

1 Answers1

0

When I start the calculation are all state values null or is there some type of initial value?

Zero is a good number for simple models, but it is not always zero. Sometimes it is possible to appeal to domain knowledge or to estimate initial values in any other way, such as a wide range of Monte Carlo methods.

Isaac
  • 101