8

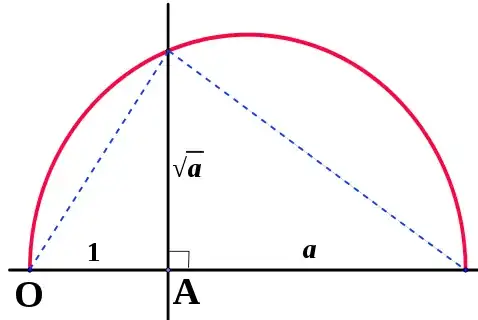
Is $2^{1/4}$ (fourth root of two) constructible using only a straight edge and compass? How would you construct it?

I understand that a number is constructible if it can be done in a finite number of step in a field.

I believe it is constructible because the degree of $Q(2^{\frac{1}{4}}$ over the rationals is $[Q(2^{1/4})): Q] = 4$, which has the form $2^k$. The degree is 4 because a basis for $2^{1/4}$ is $${1, 2^{1/4},2^{1/2}, 8^{1/4}}.$$ Is this reasoning correct?

If it is constructible, do I need to find the four roots of unity and multiple each by $2^{1/4}$? And then how do I proceed from there?

J. M. ain't a mathematician
  • 75,051
Kevin Jackson
  • 81
  • 1
  • 3
  • 8
    Just take the square root twice. https://math.stackexchange.com/questions/705/compass-and-straightedge-construction-of-the-square-root-of-a-given-line/708 – saulspatz Mar 22 '18 at 12:00

3 Answers3

26

Hint: If $a$ is constructible, then so is $\sqrt a$.

enter image description here

[image from Wikipedia]

lhf
  • 216,483
6

The construction is possible and rather straight forward.

First construct a right isosceles triangle with side of $1$

The hypotenuse is $\sqrt 2$

Extend $\sqrt 2$ by $1$ and construct a right triangle whose hypotenuse is $ 1+ \sqrt 2$ and the altitude from the the right angle divides the hypotenuse into segments of length $1$ and $\sqrt 2$

The altitude from the right angle in this triangle has length of $2^{1/4}$ as desired.

Mohammad Riazi-Kermani
  • 68,728
2

Draw a line $AB$ of length $2$, then extend it to $C$ so $AC=3$. Draw a circle with the diameter $AC$, then draw a line perpendicular to $AC$ through $B$. Let it intersect the circle, at both sides of $AC$, at $D$ and $E$.

Then, $BD=BE=\sqrt2$.

Now take $BD$ or $BE$ as the new $AB$ and repeat.

Then the new $BD$ or new $BE$ is $\sqrt[4]{2}$.

DynamoBlaze
  • 2,781
  • To clarify; in repeating the process you do not extend $BD$ or $BE$ to a point $F$ such that $BF=3$, but to a point $F$ such that $BF=\sqrt{2}+1$. – Servaes Mar 22 '18 at 14:32