It is for homework. But I am not asking the answer, since it seems to be already given in many posts like this one... I am pretty sure that I will get an A just copying and pasting it.
My question is a little bit about logic, I think.
Many texts argue that two matrices A and B commute IF AND ONLY IF they share a not null set of eigenvectors.
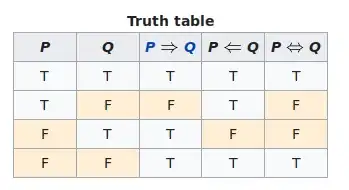
In a quick research about logic I found that $P \iff Q$ has the following truth table:
So, calling events:
$E_1$ : matrices A and B share a not null set of eigenvectors
$E_2$ : matrices A and B commute
I understand that this proof requires at least two steps:
- $E_1 \implies E_2$
- $\neg E_1 \implies \neg E_2$
The first part seems to be fulfilled by:
For a $\mathbf{A}, \mathbf{B} \in \mathbb{C}^n \times \mathbb{C}^n$, say $\{x_i\} \in \mathbb{C}^n$ is a set of vectors such that:
$\mathbf{A} {x_i} = a_i {x_i}$, where $a_i$ is a eigenvalue of $\mathbf{A}$
$\mathbf{B} {x_i} = b_i {x_i}$, where $b_i$ is a eigenvalue of $\mathbf{B}$
Then we can see that:
$\mathbf{B}(\mathbf{A} x_i) = \mathbf{B}(a_i x_i) = a_i(\mathbf{B} x_i) = a_i b_i x_i$
$\mathbf{A}(\mathbf{B} x_i) = \mathbf{A}(b_i x_i) = b_i(\mathbf{A} x_i) = a_i b_i x_i$
I see it in in much more precise shapes and in many places.
How to show the second part? Is it necessary right?
Given $\mathbf{A}, \mathbf{B} \in \mathbb{C}^n \times \mathbb{C}^n$
If, for some $y \in \mathbb{C}^n$:
$\nexists \lambda \in \mathbb{C} | \mathbf{A} y = \lambda y$
Then:
$\mathbf{B} (\mathbf{A} y) \neq \mathbf{A} (\mathbf{B} y)$