Proof of sum formula, no induction

Question

$$\sum_{k=1}^n k=\frac{n(n+1)}2$$

So I was trying to prove this sum formula without induction. I got some tips from my textbook and got this.

Let $S=1+2+\cdots+n-1+n$ be the sum of integers and $S=n+(n+1)+\cdots+2+1$ written backwards. If I add these $2$ equations I get $2S=(1+n)+(1+n)\cdots(1+n)+(1+n)$ $n$ times.

This gives me $2S=n(n+1) \Rightarrow S=\frac{n(n+1)}2$ as wanted.

However if I changed this proof so that n was strictly odd or strictly even, how might I got about this. I realize even means n must be $n/2$. But I haven't been able to implement this in the proof correctly.

Edit: error in question fixed, also by $n/2$ I mean should I implement this idea somewhere in the proof, cause even means divisible by $2$.

Answer 1

For $n$ even i.e. $n=2m$ for some $m\in\mathbb{N}$. Let $S:=1+2+...+2m$ then

$$2S=S+S=(1+2+...+(2m-1)+2m)+(2m+(2m-1)+...+2+1)=((1+2m)+(2+(2m-1))+...+((2m-1)+2)+(2m+1))=\underbrace{((2m+1)+...+(2m+1))}_{2m-times}=(2m+1)\cdot 2m$$ Therefore $$S=\frac{(2m+1)2m}{2}=m(2m+1)$$ Analogue for $n$ odd. The formula is the same as in general for any $n$. You indeed just substitute directly into it. For instance $$\frac{n(n+1)}{2}\Rightarrow \frac{2m(2m+1)}{2}=m(2m+1)$$

Answer 2

Method 1: (requires you to consider whether $n$ is odd or even.)

$S = 1 + 2 + ...... + n$.

Join up the first to term to the last term and second to second to last and so on.

$S = \underbrace{1 + \underbrace{2 + \underbrace{3 +....+(n-2)} + (n-1)} + n}$.

$= (n+1) + (n+1) + .....$.

If $n$ is even then:

$S = \underbrace{1 + \underbrace{2 + \underbrace{3 +..+\underbrace{\frac n2 + (\frac n2 + 1)}+..+(n-2)} + (n-1)} + n}$

And you have $\frac n2$ pairs that add up to $n+1$. So the sum is $S= \frac n2(n+1)$.

If $n$ is odd then:

$S = \underbrace{1 + \underbrace{2 + \underbrace{3 +..+\underbrace{\frac {n-1}2 + [\frac {n+1}2] + (\frac {n+1}2 + 1)}+..+(n-2)} + (n-1)} + n}$

And you have $\frac {n-1}2$ pairs that also add up to $n+1$ and one extra number $\frac {n+1}2$ which didn't fit into any pair. So the sum is $\frac {n-1}2(n+1) + \frac {n+1}2 =(n-1)\frac {n+1}2 + \frac {n+1}2 = (n-1 + 1)\frac {n+1}2n=n\frac {n+1}2$.

Method 1$\frac 12$ (Same as above but waves hands over doing tso cases).

$S = average*\text{number of terms} = average*n$.

Now the average of $1$ and $n$ is $\frac {n+1}2$ and the average of $2$ and $n-1$ is $\frac {n+1}2$ and so on. So the average of all of them together is $\frac {n+1}2$. So $S = \frac {n+1}2n$.

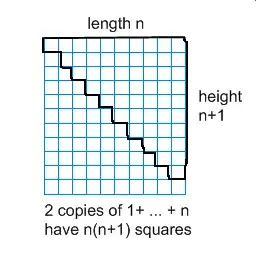
Method 2: (doesn't require considering whether $n$ is odd or even).

$S = 1 + 2 + 3 + ...... + n$

$S = n + (n-1) + (n-2) + ...... + 1$.

$2S = S+S = (n+ 1) + (n+1) + ..... + (n+1) = n(n+1)$>

$S = \frac {n(n+1)}2$.

Note that by adding $S$ to itself this doesn't matter whether $n$ is even or odd.

And lest you are wondering why can we be so sure that $n(n+1)$ must be even (we constructed it so it must be true... but why?) we simply note that one of $n$ or $n+1$ must be even.

So no problem.

Answer 3

This classical result can be also easily proved by the following trick

An extended discussion also for more general cases here How Are the Solutions for Finite Sums of Natural Numbers Derived?

Answer 4

A combinatorial proof. Consider the two element subsets of $\Omega=\{0,1,\dotsc,n\}$. There are $\binom{n+1}{2}$ of them (corresponding to the right hand side of the equality). But we can count in another way. Classify the two element subsets based on their maximum element. For $1\leq k \leq n$, there are $\binom{k}{1}=k$ two element subsets whose maximum element is $k$ since there are $k$ non-negative integers less than $k$.

Another proof based on telescoping. Let $n^{\underline{2}}=n(n-1)$ (this is the falling factorial of length two. The exponent has an underline for notation). Observe that $$ \frac{1}{2}(n+1)^{\underline{2}}-\frac{1}{2}(n)^{\underline{2}}=n. $$ In particular $$ \sum_{k=1}^nk=\frac{1}{2}\sum_{k=1}^n (k+1)^{\underline{2}}-(k)^{\underline{2}}=\frac{(n+1)^{\underline{2}}}{2}=\frac{n(n+1)}{2}. $$