I found in a book of Sangakus the following problem.
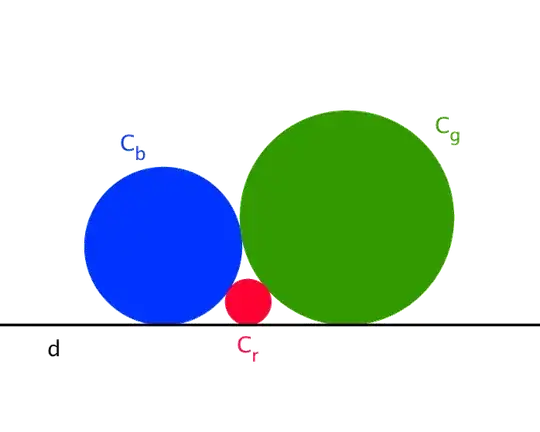
Let $R_b$, $R_g$ and $R_r$ the radiuses of the blue, green and red circles $C_b$, $C_g$ and $C_r$.
Prove that $$\frac{1}{\sqrt{R_r}}=\frac{1}{\sqrt{R_b}}+\frac{1}{\sqrt{R_g}}\,.\quad (1)$$ And this I can do. But then
I would like to draw the figure myself with only a ruler and a compass.
I know it is possible as I can construct inverses, sums and square roots with only a ruler and a compass, but when I tried to draw the figure with a "simple" or "natural" construction, I failed.
Does someone have an idea of how to draw it "naturally"?
EDIT
Answer to a comment of Amzoti:
To prove Relation (1) I first prove the relation:
$$AB^2=4R_gR_b\quad (2)$$
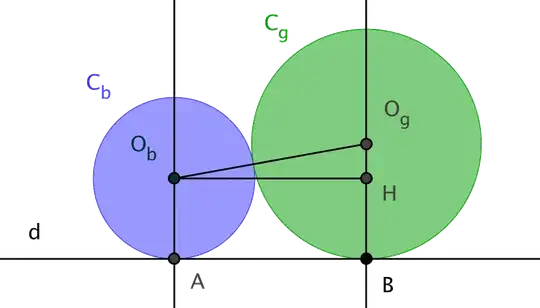 Relation (2) is a consequence of Pythagoras' theorem in the triangle $O_bO_gH$:
$$AB^2+(R_g-R_b)^2=(R_b+R_g)^2\,.$$
(It was the previous Sengaku in the book.)
Relation (2) is a consequence of Pythagoras' theorem in the triangle $O_bO_gH$:
$$AB^2+(R_g-R_b)^2=(R_b+R_g)^2\,.$$
(It was the previous Sengaku in the book.)
We thus get the relations $$ \begin{align} AB^2 & =4R_gR_b\quad (2) \\ AC^2 & =4R_gR_r\quad (3) \\ BC^2 & =4R_bR_r\quad (4) \\ \end{align} $$ where $A$, $B$, $C$ are the orthogonal projections of the centers of the circles $C_b$, $C_g$ and $C_r$ on the line $d$. The relation $AB^2=AC^2+BC^2+2AC.BC$ then yields, using Relations (2) to (4), $$4R_gR_b=4R_gR_r+4R_bR_r+8\sqrt{R_bR_g}R_r$$ Divided by $4R_rR_gR_b$ this equation is $$\frac{1}{R_r}=\Big(\frac{\sqrt{R_g}+\sqrt{R_b}}{\sqrt{R_bR_g}}\Big)^2$$ which is in fact Relation (1) squared.
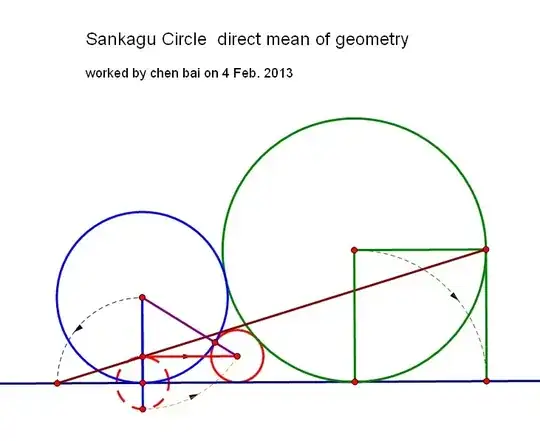
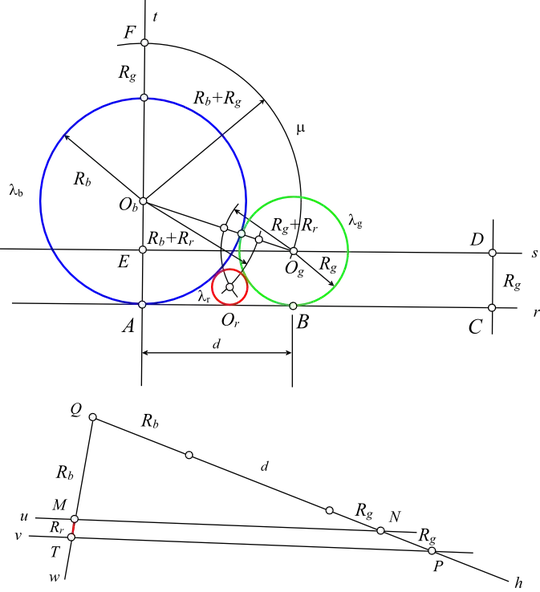
![enter image description here]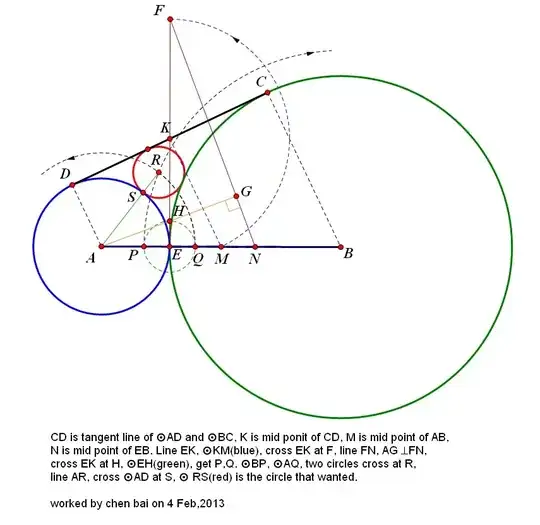
I don't know much about geometry and I didn't know this Apollonius' problem, it is true that the problem I quoted above can be seen as one of the limit cases of Apollonius' problem, the case with two circles and one line. And indeed the general problem of Apollonius is very interesting! Thanks for your comment. – Sebastien B Jan 04 '13 at 17:53