Volume of a sphere using geometry

Question

How to derive the formula for the volume of a sphere using geometry?

$V = (4/3) \pi r^3$

Edit: How did Archimedes calculate the volume of a sphere? Integration wouldn't have been there at his time.

There is similiar question.http://math.stackexchange.com/questions/106553/volumes-of-cones-spheres-and-cylinders/166132#166132 You can check my visual answer. — Mathlover, Jan 03 '13 at 20:05
@Mathlover : I couldn't understand after that /pi(r^2 - h^2) of sphere :( Aren't you indirectly integrating it? — Inquisitive, Jan 03 '13 at 20:11
In the second picture,the disk area that be cut is equal to sphere volume. — Mathlover, Jan 03 '13 at 20:21
I believe he knew this level integrating technics.This is just thinking in geometry and comparing areas in two different matters — Mathlover, Jan 03 '13 at 20:25
Cf. the question Can the Surface Area of a Sphere be found without using Integration? — Américo Tavares, Jan 03 '13 at 21:01

Chris Taylor · Accepted Answer · 2013-01-03T20:51:54.827

Consider a sphere of radius $r$, and a cone of radius $2r$ and height $2r$.

Slice the cone into circles a distance $x$ below the apex of the cone. The circle at distance $x$ has radius $x$, and hence area $\pi x^2$.

Place the sphere on a level surface, and slice it into circles a distance $x$ above the surface. The radius of such a circle is $\sqrt{x(2r-x)}$, and hence its area is $2\pi xr - \pi x^2$.

Note that the sum of the areas of these circles (one from the cone and one from the sphere) is $2\pi xr$. If you hang them one one side of a balance, a distance $2r$ from the fulcrum, then the total moment is $2r \times 2\pi xr = 4\pi r^2x$.

They can therefore be balanced by a circle of area $4\pi r^2$ (and hence of radius $2r$) a distance $x$ from the fulcrum. Taken together, all these circles make up a cylinder of radius $2r$ and height $2r$.

The preceding five paragraphs are summarized in this picture, where all of the red lines have the same length, and the two gray circles on the left of the fulcrum balance the one on the right.

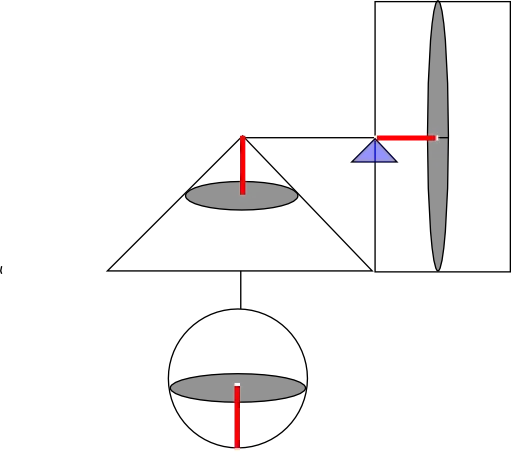
enter image description here

You can consider all the mass of the cylinder to be concentrated at its center of mass, which is a distance $r$ from the fulcrum. By the leverage principle, the volume of the sphere plus the cone must be equal to the half the volume of the cylinder. The volume of the cylinder and cone are known to be

$$V_{{\rm cylinder}} = {\rm base} \times {\rm height} = 4\pi r^2 \times 2r = 8\pi r^3$$

$$V_{{\rm cone}} = \frac{1}{3} \times {\rm base} \times {\rm height} = \frac{1}{3} \times 4\pi r^2 \times 2r = \frac{8}{3}\pi r^3$$

We therefore have

$$V_{\rm sphere} + V_{\rm cone} = \frac{1}{2} V_{\rm cylinder}$$

and hence

$$V_{{\rm sphere}} = \frac{1}{2}V_{\rm cylinder} - V_{\rm cone} = 4\pi r^3 - \frac{8}{3}\pi r^3 = \frac{4}{3}\pi r^3$$

QED

if you slice the cone at distance x from the apex/base then it would be a single circle, not circles, right? — Rayhunter, Jan 31 '18 at 19:51

score 2 · Answer 2 · answered Jan 03 '13 at 19:33

2

Archimedes was able to compare the volumes of semisphere cylinder and cone of radius $r$ and height $r$ by the Cavalieri principle. (cf. his tombstone)

answered Jan 03 '13 at 19:33

Hagen von Eitzen

374,180

Volume of a sphere using geometry

2 Answers2