2

I have come across the function $\sin^{x}(x)$ (or a in a different notation$(\sin(x)^{x})$ while practicing calculating its the first derivative. I then plot it in Desmos since I don't know how to graph this by hands yet. It seems that the graphing device suggests this function is discontinuous between the interval $[\pi ,2\pi ]$. The graph is also peculiar between the interval $[0 ,\pi ]$, while replicating itself for any interval $(2\pi ,3\pi )$, $(3\pi ,4\pi )$, $(5\pi ,6\pi )$, etc.

The behaviour of this function on the entire interval $(-\infty ,0)$ is also interesting. It doesn't look anywhere similar to $[0,+∞)$.

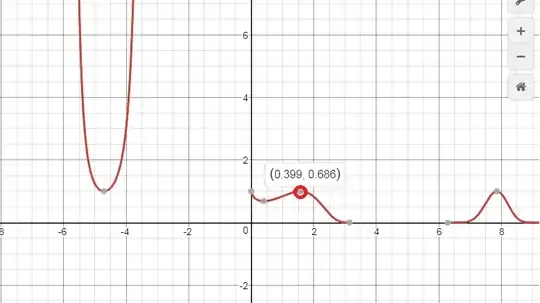
The first derivative of this function is $\sin^{x}(x)+\ln(\sin(x))+\frac{x\cos(x)}{\sin(x)}$. As with most other complex transcendental functions, this is not a simple derivative to work with. Could you show me some strategies to explore and graph this function manually. I would like to particularly find the red circle point found on this graph:

graph of sin^x(x)

I have also tried to plot this on Wolfram and its shape is similar. Is this an accurate shape at all or is the graphing device errorneous somehow?

ChoF
  • 1,740
James Warthington
  • 3,187
  • Raising negative numbers to arbitrary real numbers doesn't work well over the reals. They're saying the function is undefined. – saulspatz Mar 15 '18 at 00:02
  • $\sin x$ is negative on these intervals – Tob Ernack Mar 15 '18 at 00:02
  • The point circled in red is certainly not $(0.399,0.686)$. It looks more like $(\pi/2,1)$ – MasB Mar 15 '18 at 00:14
  • You are right, the point $ (0.399,0.686)$ should be the point right next to the left hand side. Is there a way to find out this point? – James Warthington Mar 15 '18 at 01:00
  • "Raising negative numbers to arbitrary real numbers doesn't work well over the reals. They're saying the function is undefined." I am not sure what does it mean by this? Isn't negative exponentiation of x^-x is simply 1/x^x? Or do you mean exponentiation operator as suggested in this thread: https://math.stackexchange.com/questions/317528/how-do-you-compute-negative-numbers-to-fractional-powers – James Warthington Mar 15 '18 at 01:00

2 Answers2

5

The canonical way to define a power $a^b$ is to do $$ a^b:=e^{b\log a}. $$ This works great, but the problem is that it doesn't make sense when $a<0$. And that's the state of things. There is no natural way to define arbitrary powers of negative numbers (think $(-1)^{1/2}$ for an easy example).

So your function is not defined whenever $\sin x<0$, which is all the intervals $((2k-1)\pi,2k\pi)$. That's why your graph has so many gaps.

On the left axis, you have negative powers of $\sin x$, and that's why you get the asymptotic behaviour towards $x=-k\pi$, $k\in\mathbb N$.

I don't think you can expect to find the roots of the derivative analytically. At best, you could try Newton's method.

Martin Argerami
  • 205,756
0

Note that the function is not defined on reals for

  • $\sin x=x=0$ (but $\sin^x x \to 1$ for $x\to o^+$)
  • $\sin x<0$ (negative base is not well defined)
user
  • 154,566