3

$\color{red}{\text{Ordinary definition}: }$Let $f(u,v)$ be the angle (note that $0\leq f\leq \pi$) between the vectors $u$ and $v$ in $\mathbb{R}^2$, uniquely determined by: $$\cos(f(u,v))=\dfrac{\langle u,v\rangle }{||u|| ||v||}.$$

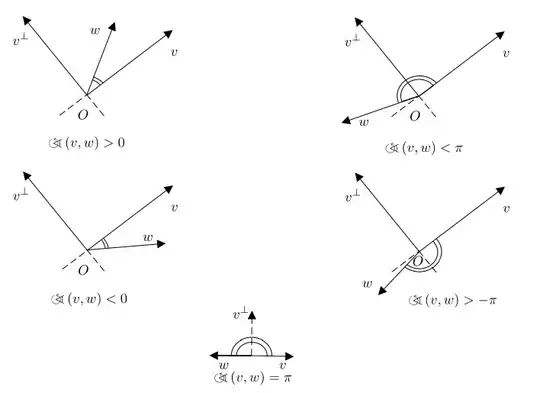
$\color{blue}{\text{Oriented angle definition:}}$ Let $u = (u_1, u_2)$ be a vector in $\mathbb{R}^2$ and define $u^{I} = (-u_2,u_1)$. Then the oriented angle, $a(u,v)$ between two vectors $u$ and $v$ in $\mathbb{R^2}$ is given by:

$a(u,v) = f(u,v)$ if $\langle u^{I},v \rangle \geq0$

$a(u,v) = -f(u,v)$ if $\langle u^{I},v \rangle < 0$

Note that $a \in \ (-\pi,\pi]$

It would appear that this definition cares about whether or not $v$ has "rotated" around $u$ and whether or not that "rotation" was clockwise or not. I don't know whether that's clear/correct, though. Here are some examples:

Community
  • 1
Matheus Andrade
  • 6,773
  • This isn’t the “usual” definition? What’s the usual definition? – rschwieb Mar 13 '18 at 14:13
  • @rschwieb the "ordinary" definition only gives angles between $0$ and $\pi$, as opposed to this one, where the "oriented" angle can take on every value between $-\pi$ and $\pi$ (not including $-\pi$). – Matheus Andrade Mar 13 '18 at 14:15
  • 1
    Your definition does what you want alright. We indeed need oriented angles sometimes. But what is the question? – Christian Blatter Mar 13 '18 at 15:01
  • It's not actually my definition, I read it in a text and wanted to understand the differences between it and the usual definition (and that's really the question here). – Matheus Andrade Mar 13 '18 at 15:03
  • @MatheusAndrade I think by now the situation is clear: we don't understand exactly what you mean by "ordinary definition." You should write that one out in detail for comparison, instead of making everybody guess what it is. How can you do oriented angles without signs? – rschwieb Mar 13 '18 at 15:32
  • @rschwieb Thank you for clearing that up. I've edited my post and hope my question can be more easily understood now. – Matheus Andrade Mar 13 '18 at 15:43
  • @MatheusAndrade Ah, I see another part of the problem. I thought your question said "how does this definition of oriented angle differ from the usual definition [of oriented angle]?" when perhaps it is actually "How does this definition of oriented angle differ from the usual definition [of the angle between two vectors]?" Thanks for clarifying. – rschwieb Mar 13 '18 at 17:14
  • 1
    Oh, I didn't think of that. The usual one to me was always the standard, non-oriented one, and I didn't even stop to think of the implicit context you pointed out. I'll edit the title promptly, thanks. – Matheus Andrade Mar 13 '18 at 17:17
  • @MatheusAndrade What text did you get the oriented angle definition from? – Galen Jun 26 '21 at 04:12
  • @Galen From a brasilian textbook by Walcy dos Santos. If you want it I could probably send it to you but don't know how much use it would be since it's in portuguese. – Matheus Andrade Jun 27 '21 at 04:00
  • @MatheusAndrade perhaps not. If you, or anyone else, would cite a book in English with an equivalent definition I would appreciate it. – Galen Jun 27 '21 at 21:23

1 Answers1

1

Assigning an angle between $0$ and $\pi$ is not sufficient to provide an orientation for the angle.

Orientation provides information about the position of two objects with respect to each other. For example, if we are standing on the equator, 10 meters between us, then saying "I am 10 meters from you" is insufficient orientation information. It would be necessary to say "I am 10 meters west of you," or "-10 meters east of you" or something that. And then you would be able to say "I am 10 meters east of you." The point of reference matters.

So for angles in a plane, simply measuring the non-reflex angle between the two suffers from this problem. You really need a sign and a convention to clear things up. Typically we use the right-hand rule so that measuring in a counterclockwise direction from the first to the second is positive. Reversing the order of the characters in the pair will reverse the orientation between the two.

rschwieb
  • 153,510
  • Can one define orientation purely in terms of Hilbert’s axioms for Euclidean geometry? – Transcendental Sep 06 '19 at 06:28
  • @Transcendental is that not inherent in his ordering axioms? – rschwieb Sep 06 '19 at 14:32
  • Well, it isn’t obvious to me how one can define orientation using Hilbert’s axioms alone so that given two arbitrary distinct rays $ l $ and $ m $ with the same starting point, one can immediately determine if $ l $ is oriented clockwise or anticlockwise with respect to $ m $. – Transcendental Sep 08 '19 at 03:03