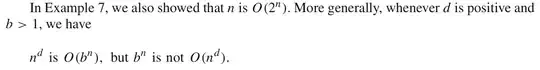How to prove that $n^d$ is $O(b^n)$ from $n$ is $O(2^n)$, given that $d>0, b>1$?

Question

I'm reading Rosen's Discrete Mathematics and Its Application, at Page 212, it's about the "Big-O" notation using in computer science.

This is the description in the book:

And here is my reasoning:

Since there wasn't a program with "negative" steps, I only consider the case $n>0$.

With $n$ is $O(2^n)$, there exist two constants $C$ and $k$ such that $$n \le C \cdot 2^n, \text{when } n>k.$$

Now take logarithms on both side we have $$\log{n} \le \log{C} + n$$

Multiply both side with $d$, we get $$d \cdot \log{n} \le d\cdot \log{C} + d \cdot n,$$

Then I stuck.

Please give me some hints about how to do next... Thanks a lot!

Answer 1

Here is one possible clever approach:

Note that from $n \in O(2^n)$ as $n \to \infty$ we immediately get $n^c \in O(2^{n^c})$ as $n \to \infty$ for any $c>0$.

Let $a = \log_2(b) > 0$.

Then $2^{an} = b^n$.

Thus $(n^c)^{d/c} \in O(2^{n^c})^{d/c} \subseteq O(2^{an})$ if we can find $c > 0$ such that $n^c·d/c < an$ as $n \to \infty$.

Can you find such a suitable $c$? If so, you are done! I'll leave you to fill in the details. $\ddot\smile$

Answer 2

A preferable way to me:

Prop: for $c \geq 0$ finite, with $f,g:\mathbb{R}\rightarrow\mathbb{R^+}$ if $$ \lim_{n\rightarrow\infty}\frac{f(n)}{g(n)} \leq c $$ then $ f \in O(g) $.

Intuitively, this makes sense: for large enough $n$, you get $f(n) \lesssim cg(n)$, which implies $f\in O(g)$. (Note its converse doesn't hold, e.g. see here)

Then you get that

Cor: for real $b>1$, $d>0$, we have that $n^d \in O(b^n)$.

Proof: we just have to show the proposition above applies. Assume $n > 1$. We apply L'Hopital's rule repeatedly. Let $k\in\mathbb{N}$ be such that $q=d-k < 0$. This exists because $d>0$. We apply the rule $k$ times: \begin{align} \lim_{n\rightarrow\infty}\frac{n^d}{b^n} &= \lim_{n\rightarrow\infty}\frac{dn^{d-1}}{\ln(b)b^n} \\ &= \vdots \\ &= \frac{d!/(d-k)!}{(\ln b)^k} \lim_{n\rightarrow\infty}\frac{n^{d-k}}{b^n} \\ &= \frac{d!/(d-k)!}{(\ln b)^k} \lim_{n\rightarrow\infty}\underbrace{\frac{1}{n^{-q}b^n}}_{-q \geq 0} \\ &\leq \frac{d!/(d-k)!}{(\ln b)^k} \lim_{n\rightarrow\infty}\frac{1}{b^n} \\ &= 0 \end{align}

See also this and this.

---

I also tried to complete your work, but an issue occurs. Not sure if this approach below is correct in all cases anyway. Let $ \tilde{c} = d\log_b C $ and $k = \log_b 2^d$.

\begin{align} n &\leq C 2^n \\ \log_b n &\leq \log_b C + n\log_b 2 \\ \log_b n^d &\leq d\log_b C + n\log_b 2^d \\ \log_b n^d &\leq \tilde{c} + kn \\ n^d &\leq b^{\tilde{c}} b^{kn} \\ \frac{n^{d/k}}{b^{\tilde{c}/k}} &= \frac{n^{d/k}}{s} \leq b^n \\ n^{d/k} &\leq s b^n \end{align} Since $d >0$, we must have $k>0$.

Case 1: $k \in (0,1]$. Then $n^d < n^{d/k} \leq sb^n$. So it's true for such $k$.

Case 2: $k > 1$. Then $ n^{d/k} \leq n^d $. It's not immediately clear to me how to easily get $ n^{d/k} \leq b^n$ from here though.