@Michael's answer identifies the error, but I thought I'd provide a comprehensive diagram. (It's kinda what I do.)
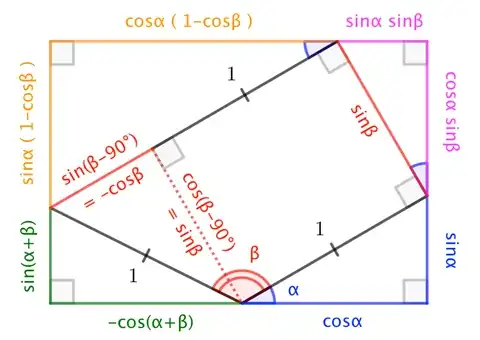
This shows
$$\begin{align}
\sin(\alpha + \beta) &= \sin\alpha + \cos\alpha \sin\beta - \sin\alpha(1-\cos\beta) = \phantom{-\left(\;\right.}\sin\alpha \cos\beta + \cos\alpha \sin\beta \phantom{\left.\;\right)} \\
-\cos(\alpha+\beta) &= \cos\alpha(1-\cos\beta) + \sin\alpha \sin\beta - \cos\alpha = -\left(\;\cos\alpha\cos\beta - \sin\alpha\sin\beta\right)\;
\end{align}$$
Note: The figure is valid even for non-obtuse $\beta$ (or non-acute $\alpha$), provided appropriate consideration is given to signed lengths.
Note 2: OP (and others) may be interested in a related figure of my own.

