18

Suppose the path-avoiding snail walks along the grid according to the following algorithm:

  1. At each step, the snail steps unit distance if doing so will not collide with its trail.
  2. If a step of unit distance will collide with the trail, the snail moves half way toward the trail.
  3. After each step, the snail turns right or left or remains straight.

Let $a(n)$ be the minimal number of steps required before the snail can have a step size of $(2n-1)/2^k$ for some $k$ such that the fraction is reduced.

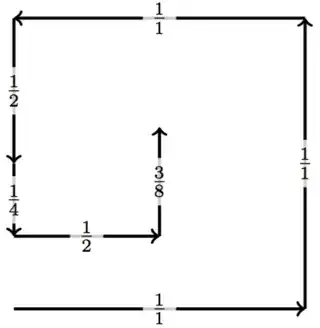
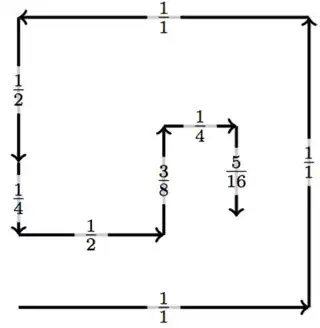
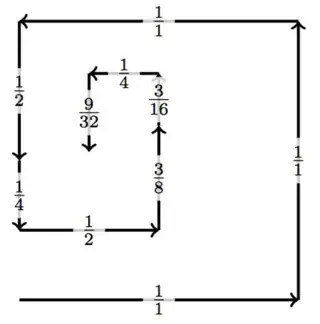
Here are a few examples of minimal walks (solved by brute force):

Step size 3/8 in 7 steps Step size 5/16 in 9 steps Step size 7/16 in 8 steps Step size 9/32 in 10 steps

This shows that you can have a step size with numerator $3$ in $7$ steps, numerator $5$ in $9$ steps, numerator $7$ in $8$ steps, and numerator $9$ in 10 steps—therefore $a(2) = 7$, $a(3) = 9$, $a(4) = 8$ and $a(5) = 10$.

Is there a general strategy of determining $a(n)$?

Also, given a random walk (where the turns are chosen uniformly at random) what is the expected number of steps before the snail takes a step of $(2n-1)/2^k$ for some $k$?

Known values (assuming the implementation is correct):

a(2) = 7      a(9)  = 11    a(16) = 10    a(23) = 12    a(30) = 13
a(3) = 9      a(10) = 12    a(17) = 12    a(24) = 13    a(31) = 12
a(4) = 8      a(11) = 11    a(18) = 13    a(25) = 12    a(32) = 11
a(5) = 10     a(12) = 12    a(19) = 14    a(26) = 13    a(33) = 13
a(6) = 11     a(13) = 11    a(20) = 13    a(27) = 14    a(34) = 14
a(7) = 10     a(14) = 12    a(21) = 13    a(28) = 13    a(35) > 14
a(8) = 9      a(15) = 11    a(22) = 14    a(29) = 12

Here are some walks for $n=20$, $n=21$, and $n=22$:

n = 20: (0,0)--(1,0)--(1,1)--(0,1)--(0,1/2)--(0,1/4)--(1/2,1/4)--(1/2,5/8)--(1/2,13/16)--(1/4,13/16)--(1/4,17/32)--(1/4,25/64)--(1/8,25/64)--(1/8,89/128)
n = 21: (0,0)--(1,0)--(1,1)--(0,1)--(0,1/2)--(0,1/4)--(1/2,1/4)--(1/2,1/8)--(3/4,1/8)--(3/4,9/16)--(3/4,25/32)--(3/4,57/64)--(3/8,57/64)--(3/8,73/128)
n = 22: (0,0)--(1,0)--(1,1)--(0,1)--(0,1/2)--(0,1/4)--(1/2,1/4)--(1/2,5/8)--(1/4,5/8)--(1/4,7/16)--(1/4,11/32)--(1/8,11/32)--(1/8,43/64)--(9/16,43/64)--(9/16,43/128)
Peter Kagey
  • 5,052
  • 2
    I've added this to the OEIS as A300444. – Peter Kagey Mar 06 '18 at 05:08
  • 3
    It would be useful to see your source code, or paths (even as a string of {L,R,S}) for some of your larger indices there. – user24142 Mar 07 '18 at 06:15
  • It would indeed be interesting to see the paths, especially for $n=20,21,22$. – evgeny Mar 15 '18 at 20:45
  • There may be a loose connection here to Fusible numbers, since some of the operations involved are very similar; see https://math.stackexchange.com/questions/40404/proof-of-recursive-formula-for-fusible-numbers for some pointers there. – Steven Stadnicki Mar 17 '18 at 16:17

1 Answers1

1

I have no idea about proving maximality, which is probably very difficuly, but the following construction gives an answer that coincides with OP's calculation if $n \leqslant 34$ except for $n=11, 21, 22, 23$, and its slight modification is ok for $n=11, 23$, but not $n=21, 22$.

Game. Consider such a game: we have two natural numbers $(f, b)$ and two types of operations -- to $(f/2, b+f/2)$ (if $f/2$ is natural) and to $(b, f)$. Starting position is $(2^{d(n-1)+1}, 0)$, final position is $(2n-1, \ldots)$, the goal is to get there with minimal number of operations.

The minimal sequence of operations may be reconstructed backwards, doing inverse to the first operation when possible, and inverse of the second otherwise, and consists of $1+d(n-1)+g(n-1)$ operations, where $d(k)$ is the number of digits in binary representation on $k$ and $g(k)$ is the number of groups of repeating digits there.

Example. Consider $n=6$. Then $2^{d(n-1)+1}=16$ and $2n-1=11$, so $$(11=1011_2, 5=0101_2) \twoheadleftarrow (5=0101_2, 11=1011_2) \leftarrow (10=1010_2, 6=0110_2) \twoheadleftarrow (6=0110_2, 10=1010_2) \leftarrow (12=1100_2, 4=0100_2) \twoheadleftarrow (4=0100_2, 12=1100_2) \leftarrow (8=1000_2, 8=1000_2) \leftarrow (16=10000_2, 0)$$ is the sequence with minimal $1+d(101_2)+g(101_2)=7$ operations.

We consider $f$ as the distance forward, and $b$ -- backward, as if snail always looks vertically and alternates segments up and down. Now you can construct snail's walk as follows: make first three moves as right, up, left; then go along the sequence from the previous game, replacing first operations by moves up or down, and second - by moves right; in the end make one move up or down.

The snail's move for $n=6$.

Modification. The game may be modified as follows: we have three natural numbers $(f, b_1, b_2)$ and three types of operations -- to $(f/2, b_1+f/2, b_2+f/2)$, to $(b_1, f, 0)$ and to $(b_2, f, 0)$. Starting position is $(2^{d(n-1)+1}, 0, 0)$, final position is $(2n-1, \ldots, \ldots)$, the goal is the same.

Here we consider $b_1$ and $b_2$ as distances backward along left and right sides of snail. Second and third operations should be interpreted as moves left or right according to the situation.

Unfortunately, I can not solve modified game, but computer simulation obtains the same solutions as OP's for $n=11, 23$, but $a(21)=14>13$ and $a(22)=15>14$.

Comment. Feel free to correct my language!

evgeny
  • 3,781