9

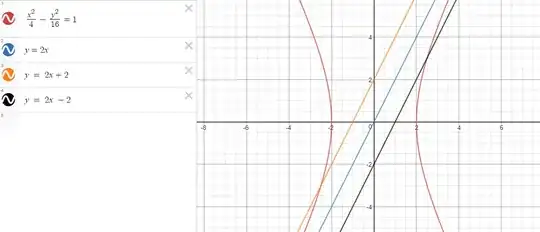
A hyperbola has equation $\frac{x^2}{4}-\frac{y^2}{16}=1$. Show that every other line parallel to this asymptote, $y=2x$, intersects the hyperbola exactly once.

enter image description here

So here's the hyperbola. The blue line represents the asymptote $y = 2x$. I am not concerned with the other asymptote that has a negative gradient, $y =-2x$, although the same principles would apply.

Now the problem can re-phrased as:

For the line $y = 2x+c , c \ne 0$

Prove the line intersects the hyperbola once exactly for any non-zero c.

The orange line represents the case where $c>0$.

The black line represents the case where $c<0$.

This is geometrically intuitive, however, I am struggling to prove this algebraically.

FIRST ATTEMPT

First of all, substitute $y = 2x+c$ into $\frac{x^2}{4}-\frac{y^2}{16}=1$ for $y$.

$\frac{x^2}{4}-\frac{(2x+c)^2}{16}=1$

Multiply through by 16.

$4x^2-(2x+c)^2=16$

$4x^2-(4x^2+4cx+c^2)=16$

$-4cx-c^2=16$

$c^2 + 4cx + 16 = 0$

Take the discriminant to determine the number of times the line intersects the hyperbola.

$\Delta = B^2 - 4AC$ for a generic quadratic $Ax^2 + Bx + C = 0$.

(Using upper case $A$, $B$ and $C$ as lower case $c$ is already taken.)

Therefore,

For $0x^2 +4cx + (c^2 + 16)=0$ where the quadratic is taken in terms of $x$.

$\Delta = (4c)^2 -4(0)(c^2 + 16) = 16c^2$

As $c \ne 0$,

$16c^2 > 0$

Hence all lines parallel to $y = 2x$ must intersect the hyperbola twice.

I've managed to disprove what I am trying to prove. Please can someone explain where I have gone wrong.

Justin
  • 2,565
  • 5
  • 20
  • 39
Inquirer
  • 825
  • 1
    i think you must solve your equation for $x$ – Dr. Sonnhard Graubner Mar 04 '18 at 13:12
  • It's interesting to note what happens to analysis of $ax^2+bx+c$ when $a=0$. The discriminant certainly comes out positive, which would normally imply two solutions, but it implies the two solutions given by the quadratic formula, and you can see what happens to them when $a=0$. – G Tony Jacobs Mar 04 '18 at 13:42

2 Answers2

12

You don't have a quadratic equation, $c^2+4cx+16=0$ is a linear equation with the single solution $x=-\frac{16+c^2}{4c}$, so there is only one intersection point when $c \ne 0$ and none when $c = 0$.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
Álvaro Serrano
  • 442
6

You are actually done at $$c^2+4cx+16=0$$

Remember that you're solving for $x$, and you get only one such $x$, unless $c=0$.

cansomeonehelpmeout
  • 12,782
  • 3
  • 22
  • 49