Why do we call things like this a function

Question

Why do we call $f(x) = \sqrt x$ a function, if by definition $y = \sqrt x$ is not a function since for included values of $x$, it gives us more than one value of $y$ considering the positive and negative answers in the radicals?

Answer 1

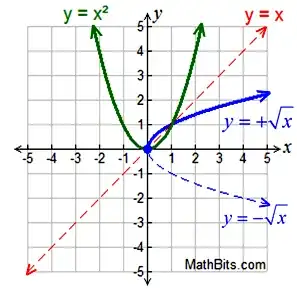
The graph of $f(x)=\sqrt{x}$ does not give more than one value of $y$ at one value of $x$, you are only taking the principal root(nonnegative root) of $\sqrt x$.

You are probably mistaking this for the equation(s) $y=\pm \sqrt x$, which is the inverse relation of $y=x^2$.

$\pm \sqrt x$ are two separate functions/equations.

Answer 2

Note that by definition,

$\forall a \ge 0, \;\;\sqrt a=b \ge 0\;$ with $b$ such that $b^2=a.$

Then we define for $x\in[0,+\infty): $

$$f(x)=\sqrt x\ge 0$$

Now, $f(x)$ is a function distinct from

$$g(x)=-\sqrt x\le 0$$

More in detail: $f(x)$ is the inverse function of $h(x)=x^2$ for $x\ge 0$ and $g(x)$ is the inverse function of $h(x)=x^2$ for $x \le 0$.

Answer 3

Consider, for instance, the two equalities $$ 2^2 = 4, \qquad (-2)^2 = 4. $$ Both $2$ and $-2$ are square roots of $4$. When we want to consider the nonnegative square root of $4$, i.e., consider only $2$ and not $-2$, we then write $$ 2 = \sqrt{4} $$ and call $2$ the principal square root of $4$.

In general, for every nonnegative real number $x$, the symbol $\sqrt{x}$ denotes the nonnegative square root of $x$, called the principal square root of $x$.

So the function $f$, given by $f(x) = \sqrt{x}$, takes any nonnegative real number $x$ and returns its principal square root (not its two square roots).