A tangent to a circle with a straight edge

Question

Given a circle on an Euclidean plane and a point $A$ outside the circle, find a line through $A$, tangent to the circle.
You're allowed to use a straight edge only.

score 4 · Accepted Answer · answered Mar 03 '18 at 11:59

Draw two lines through $A$, crossing the circle. For the next step to be possible, the lines need be in different distances from (unknown...) center of the circle.
Name the intersections of one line and a circle $B$ and $C$, for the other line: $D$ and $E$:

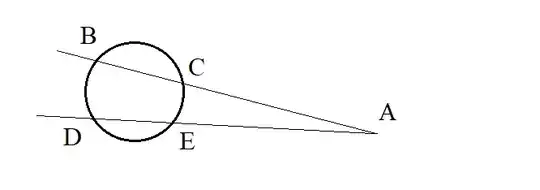
Find a point $F$ at the intersection of lines $BD$ and $CE$, and $G$ at the intersection of $BE$ and $CD$:

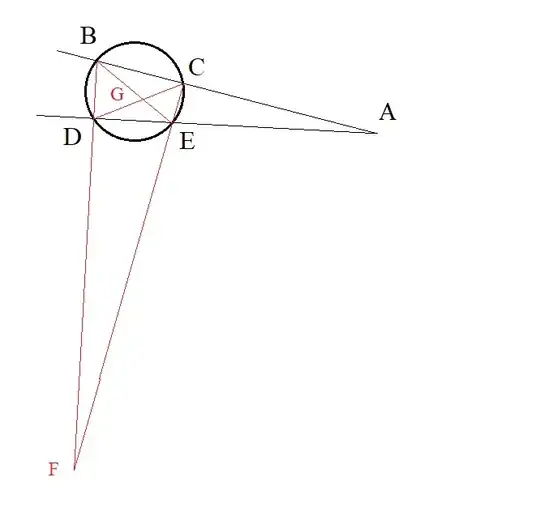
Now find $H$ and $J$ as intersections of the line $FG$ with the circle:

Voilà: lines $AH$ and $AJ$ are tangent to the circle.

I found the same solution in this answer by ccorn to the Construct tangent to a circle question by ja72. — CiaPan, Mar 04 '18 at 19:06

score 0 · Answer 2 · answered Jul 11 '18 at 16:53

0

Generally speaking, Mohr-Mascheroni theorem asserts that whatever constructible by compass and straightedge can also be constructed by straightedge only. Of course, if you want to construct a circle, you surely need to satisfy with constructing 3 distinct points on it.

answered Jul 11 '18 at 16:53

2

I suppose you meant Poncelet–Steiner theorem, not Mohr-Mascheroni...? – CiaPan Jul 11 '18 at 16:59
My bad, yes. A small arc of the circle together with the center will suffice for the general case. In your problem and various special cases, we need to be specific and get to work. Sorry. – Jul 11 '18 at 17:03
1

Well, the Poncelet–Steiner theorem assures the constructions are possible if we have a circle with its center. But in my problem the center is not given... – CiaPan Jul 11 '18 at 17:06

A tangent to a circle with a straight edge

2 Answers2

Linked