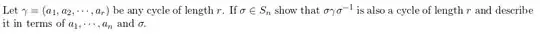Which I am attempting to answer as:
Since permutations are bijection from $X \rightarrow X$. Then $a_i = \sigma(a_j)$ for some $j$.
Assume $1 \leq i \leq r$
We get:
$\sigma\gamma\sigma^{-1}(a_i)=\sigma\gamma\sigma^{-1}(\sigma(a_j)) = \sigma\gamma(a_j)$
If $j>n$ then $\sigma\gamma(a_j)=\sigma(a_j)=a_i$
Else,
$\sigma\gamma\sigma^{-1}(a_i) = \sigma(a_{j+1})$ (although if $j=r$ then it's actually $a_1$)
This allows me to show that the final function is a cycle of length $r$ but it's not enough to express $\sigma\gamma\sigma^{-1}$ in terms of $a_1, a_n$
Is there a hint I can use to finalize the proof?