Context: I have a family of discrete-time, nonlinear, dynamical system (the same one described on this preceding question) whose expression is as follows:
$$S_{D,t}=\left\{(x,y): (x_{n+1},y_{n+1}) = \left( \Im\left(\frac{1}{(x_{n} + y_n i+1)^{t}}\right)\sin{D}, \Re\left(\frac{1}{(x_{n} + y_n i+1)^{t}}\right)\cos{D} \right)\right\}$$
Where $\Im$ and $\Re$ are the imaginary and real parts of the complex number generated by the expression $\frac{1}{(x_{n} + y_n i+1)^{t}}$. The control parameters are defined as time $t \in \Bbb N^{+}$, and Depth $D \in [0,8 \cdot 10^3] \in \Bbb N$. Usually a very small $n \lt 200$ is a good enough value to reach the associated stable $n$-orbit attractor in most of the cases. The rest of cases do not arrive to a stable orbit, and remain in a chaotic absorbing area. The initial condition I use for testing is $(x_0,y_0)=(0,0)$, but initially it does not matter which seed I use because I am arriving to the same similar periodic orbits, as far as the control parameters are fixed.
The dynamical system is nonlinear and it is non continuous.
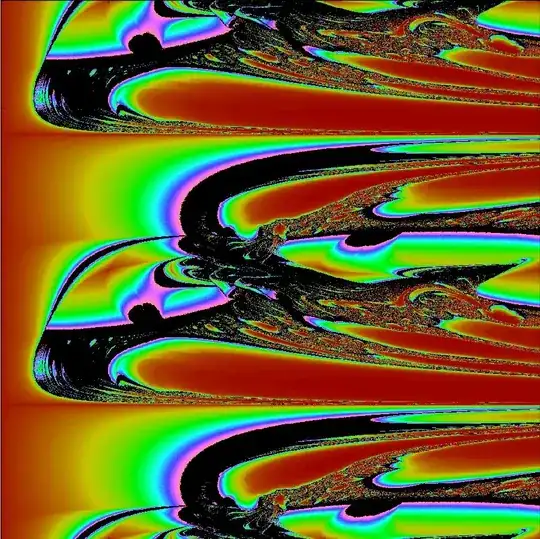
The fact is that $sin(D)$ is sampling the more broader non-discrete continuous expression $sin{(\alpha)}, \alpha \in [0,2\pi]$. As $D$ is a natural number, $D \pmod {2 \pi}$ is equidistributed along $[0,2 \pi]$. I wanted to see how looks the relationship of $D$ and $t$ via a escape time algorithm. So the escape time algorithm for a given initial condition $(x_0,y_0)$ is how many $n$ steps are required to reach a stable orbit (if it is ever reached). As a result, the darker the color is, the quicker $(x_0,y_0)$ reaches a stable orbit for the specific combination of $D$ and $t$. The cases in black color are not able to reach a stable orbit, they stay in a chaotic absorbing area. And it looks like this:
The image shows the cases in which $(x_0=0,y_0=0)$ arrives to a stable orbit or a chaotic absorbing area, the $x$-axis is $t \in [0,10]$ and $y$-axis are the samplings of ($D \pmod{2\pi}$) along the interval $[0,2\pi]$ ($0$ is at the top and $2\pi$ is at the bottom, is the whole domain, so indeed the bottom continues naturally again in the top, is a cylindrical map).
The second image is a zoom-in of the initial image for $x$-axis $\in [5,5.5]$ and $y$-axis $\in [950,100]$ (a little leaf-like pattern at the bottom of the first image).
Question: I suspect that the escape time map is a fractal structure, I can see replication, rotation and symmetry of patterns in different infinite scales. And I can distinguish regions in which there is stability and the initial condition reaches a stable orbit, and other regions in which the initial condition will never attain a stable orbit. And in the other hand I can see frontier regions in which slight changes of $D$ or $t$ imply that the initial condition arrive to a stable orbit or not. Due to this, I think that the relationship of $D$ and $t$ is chaotic. And, if this is a fractal, I should be able to define its Fatou and Julia sets. According to the Wikipedia:
"The Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is 'regular', while on the Julia set its behavior is 'chaotic'."
It seems it fits my needs, but then Wikipedia says that Fatou and Julia sets are defined for complex rational functions and clearly my expression is not a complex rational. It is complex and has a complex division expression, but it is nonlinear and non continuous.
So can I define the Julia and Fatou, $J(S_{D,t})$ and $F(S_{D,t})$, sets of this fractal structure if it is not a complex rational function? If not, is there a similar definition for such non complex rational expressions? Basically what I would like to do is characterizing the fractal defining at least the Fatou and Julia sets or some of its properties. How can I do that? Thanks in advance.