Is this face inside or outside the Hamilton cycle?

Question

Assume a planar graph with a Hamilton cycle (depicted in green).

$\hskip2in$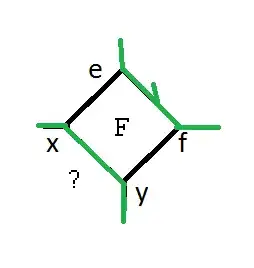 enter image description here

There are two possiblities for the displayed vertices to show up al0ng the Hamilton cycle:

$\dots ef\dots xy\dots$
$\dots ef\dots yx\dots$

What does it mean for the square $F$, if it's $xy$ or $yx$? Does this mean that it's inside or outside the Hamilton cycle? Does Grinberg's Theorem play a role here?

Intuitively ..ef..xy.. should be impossible, because F cannot both be in the component of the plane that lies to the left of the cycle and the component that lies to the right. — hmakholm left over Monica, Dec 28 '12 at 14:12

score 1 · Accepted Answer · answered Dec 30 '12 at 21:03

Expanding the comment-answer by Henning Makholm: case 1 is impossible. A Hamilton cycle in a planar graph is a simple closed curve $\Gamma$ (a Jordan curve). By the Jordan curve theorem $\Gamma$ divides the plane into two regions: bounded $B$ and unbounded $U$. The region $B$ is homeomorphic to a disk by the Schoenflies theorem. The orientation of $B$ induces positive orientation of its boundary $\Gamma$, formalizing the intuitive notion of "$B$ stays to the left of its boundary". Since the square $F$ is either in $B$ or in the complement of $B$, case 1 is inconsistent with such orientation.

Thanks for setteling the case. Would be glad if you could have a look at the linked one... — draks ..., Dec 31 '12 at 12:57

Is this face inside or outside the Hamilton cycle?

1 Answers1

Linked