Fair amount of detail if all written out. However, what it comes down to is that, using Vieta Jumping, in the first quadrant, if there are any integer solutions to
$$ x^2 - Bxy + y^2 = -2(B+1), $$
then there must be integer solutions, Hurwitz's Fundamental Solutions, in the bounded arc with between the point of minimum $y$ and the point of minimum $x,$ meaning in
$$ x \geq \frac{2y}{B} $$ and
$$ y \geq \frac{2x}{B} $$
In the picture, we see integer points $(3,1)$ and $(1,3)$ between the slanted lines.
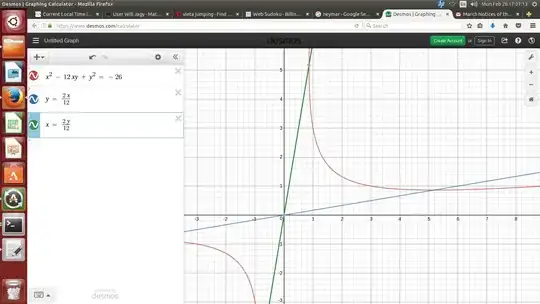 However, when $B > 12,$ and we ask about the smaller value of $x,$ we find that it is
$$ \frac{4B+6}{B + \sqrt{B^2 - 8B -12}} $$ and
$$ 2 < \frac{4B+6}{B + \sqrt{B^2 - 8B -12}} < 3 $$
However, when $B > 12,$ and we ask about the smaller value of $x,$ we find that it is
$$ \frac{4B+6}{B + \sqrt{B^2 - 8B -12}} $$ and
$$ 2 < \frac{4B+6}{B + \sqrt{B^2 - 8B -12}} < 3 $$
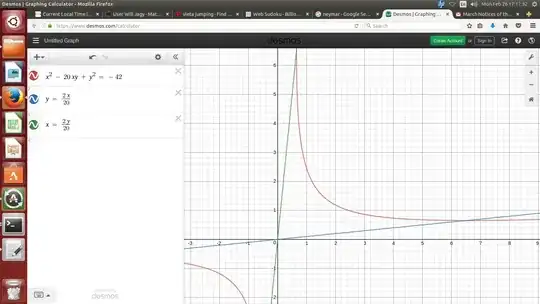 In turn, this means that there are no integer points on the arc between the slanted lines, and no integer points at all, when $B > 12.$
In turn, this means that there are no integer points on the arc between the slanted lines, and no integer points at all, when $B > 12.$
Vieta Jumping is just a means to an end. The important stuff is the collection of inequalities that need to be investigated. The best description is Hurwitz 1907

