-3

To prove:

$$\left(\frac{1+\sin\theta + i \cos\theta}{1 + \sin\theta -i\cos \theta}\right)^n = \cos\left(\frac{n\pi}{2}-n\theta\right)+i\sin\left(\frac{n\pi}{2}-n\theta\right)$$

I tried solving it by turning it into Euler form but it all got messed up. Please help.

Community
  • 1
pankaj kushwah
  • 3

4 Answers4

0

$$\left(\frac{1+\sin\theta+i\cos\theta}{1+\sin\theta-i\cos\theta}\right)^n=\left(\frac{2\cos^2\left(\frac{\pi}{4}-\frac{\theta}{2}\right)+2i\sin\left(\frac{\pi}{4}-\frac{\theta}{2}\right)\cos\left(\frac{\pi}{4}-\frac{\theta}{2}\right)}{2\cos^2\left(\frac{\pi}{4}-\frac{\theta}{2}\right)-2i\sin\left(\frac{\pi}{4}-\frac{\theta}{2}\right)\cos\left(\frac{\pi}{4}-\frac{\theta}{2}\right)}\right)^n=$$ $$=\left(\frac{\cos\left(\frac{\pi}{4}-\frac{\theta}{2}\right)+i\sin\left(\frac{\pi}{4}-\frac{\theta}{2}\right)}{\cos\left(\frac{\pi}{4}-\frac{\theta}{2}\right)-i\sin\left(\frac{\pi}{4}-\frac{\theta}{2}\right)}\right)^n=\left(\cos\left(\frac{\pi}{2}-\theta\right)+i\sin\left(\frac{\pi}{2}-\theta\right)\right)^n=$$ $$=\cos\left(\frac{n\pi}{2}-n\theta\right)+i\sin\left(\frac{n\pi}{2}-n\theta\right).$$

Michael Rozenberg
  • 194,933
0

Hint:

Let $1+\sin x=\cos t,\cos x=\sin t$

$$\dfrac{\sin t}{\cos t}=\dfrac{\cos x}{1+\sin x}=\dfrac{1-\tan\dfrac x2}{1+\tan\dfrac x2}=\tan\left(\dfrac\pi4-\dfrac x2\right)$$

$\implies t=?$

Now using How to prove Euler's formula: $e^{i\varphi}=\cos(\varphi) +i\sin(\varphi)$?,

$\cos t-i\sin t=\cdots=e^{-it}$

Can you take it from here?

lab bhattacharjee
  • 274,582
0

\begin{align*} \left(\frac{1+\sin\theta + i \cos\theta}{1 + \sin\theta -i\cos \theta}\right)^n&=\left(\cos\left(\frac{\pi}{2}-\theta\right)+i\sin\left(\frac{\pi}{2}-\theta\right)\right)^n \end{align*}

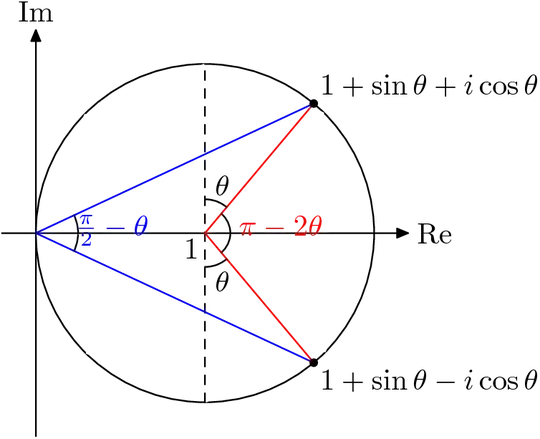
enter image description here

CY Aries
  • 23,393
0

I would start with $\frac {\pi}{2} - 2\phi = \theta$

$\left(\frac {1 + \cos 2\phi + i\sin 2\phi}{1+\cos 2\phi - i\sin 2\phi}\right)^n$

$\cos 2\phi = 2\cos^2 \phi-1$

and $\sin 2\phi = 2\sin\phi\cos\phi$

$\left(\frac {2\cos^2\phi + i2\sin\phi\cos\phi}{2\cos^2\phi - i2\sin \phi\cos\phi}\right)^n$

$\left(\frac {\cos\phi + i\sin\phi}{\cos\phi - i\sin \phi}\right)^n$

Multiply top and bottom by the conjugate of the bottom.

$(\cos\phi + i\sin\phi)^{2n}$

Apply DeMoivre's rule $(\cos 2n\phi + i\sin 2n\phi)$

Reverse the substitution $\cos n(\frac {\pi}{2}-\theta) + i\sin n(\frac \pi2 - \theta)$

Doug M
  • 57,877