Solve $3\sin^2 x - \cos^2 x - 2 =0$

Question

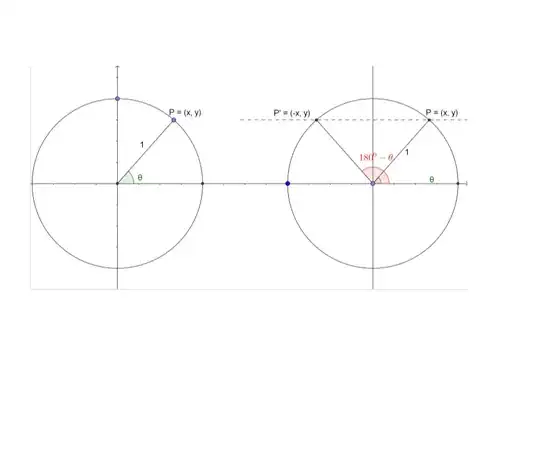
Find all the angles between $0$ and $360^\circ$ that satisfy $$3\sin^2 x - \cos^2 x - 2 =0$$

My attempt -

$3\sin^2 x - (1-\sin^2x) - 2 =0$

$ 3 \sin^2 x + \sin^2 x = 3 $

$4\sin^2 x = 3 $

$ \sin x= \frac{\sqrt{3}}{2} $

I found that $x= 60,120 $

Why is the answer for this $60,120,240,300$ ? How do I find 240 and 300?

Answer 1

Remember that when you take the square root of both sides you get $\pm$ that number. This means that $\sin(x) = \pm \frac{\sqrt{3}}{2}$. How does that change the solution?

Answer 2

hint: $\sin x = -\dfrac{\sqrt{3}}{2}$ would lead to the other two angles.

Answer 3

Hint: $y^2 = a \implies y = \color{red}{\pm}\sqrt{a}$

Answer 4

$$\sin^2x=\sin^2A\iff\cos^2x=\cos^2A\iff\tan^2x=\tan^2A$$

Using Prove $ \sin(A+B)\sin(A-B)=\sin^2A-\sin^2B $,

$$\sin^2x=\sin^2A\iff\sin(x+A)\sin(x-A)=0$$

Now $\sin(x\pm A)=0\implies x=n180^\circ\mp A$ where $n$ is any integer

Answer 5

General form of solution is :

$x=k\pi± \pi/3= k\times 180 ± 60$

$k=0 ⇒ x=0± 60 ⇒x=60,.. x=-60=300$

$k=1 ⇒ x = 180 ± 60 ⇒ x= 180+60=240, x=180-60=120$

Answer 6

The original definition of $\sin \theta$ of a right-angled triangle is just $\sin \theta =\dfrac {\text {opposite side}}{\text {hypotenuse}}$.

Later, because of its in-adequacy in handling angles larger than $90^0$, the definition is expanded to $\sin \theta = \dfrac {y-ordinate}{\text {radius of the unit circle}} = \dfrac {y-ordinate}{1}$ for the point P = (x, y).

As seen in the figure, P' = (-x, y) also satisfies that definition. Therefore, for a single valued ($\dfrac {\sqrt 3}{2}$), there corresponds two solutions of $\theta$. Another two for ($- \dfrac {\sqrt 3}{2})$.