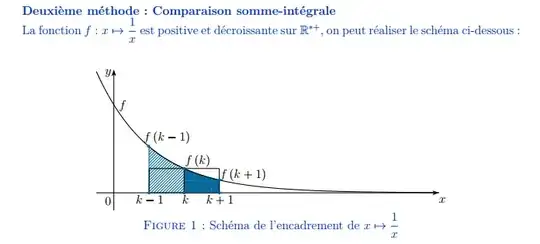
Proving $\lim \limits _{n\to \infty }\frac{1}{n^{p+1}}\sum\limits _{k=1}^{n \:}k^p=\frac{1}{p+1}$

Question

Prove that $$\lim _{n\to \infty }\frac{1}{n^{p+1}}\left(\sum _{k=1}^{n \:}k^p\:\right)=\frac{1}{p+1}$$

Mi idea was to separate the terms by saying $$\frac{\left(\sum _{n=1}^{\infty \:}n^p\:\right)}{n^{p+1}} = \left(\left(\frac{1}{n}\right)^p+\left(\frac{2}{n}\right)^p+\left(\frac{3}{n}\right)^p+...+1\right)\left(\frac{1}{n}\right)\text{ and } \lim _{n\to \infty \:}\left(\frac{1}{n}\right)=0$$

but then I got stucked in this part, an I dont know how to get it to $\displaystyle \frac{1}{p+1}$

I think you are overlapping variables, as $n$ is both in the summation and is taken as a limit. — Tommaso Seneci, Feb 13 '18 at 16:58
This is simply misworded. $\sum_{n\geq 1}n^p$ is divergent, and $\sum_{n=1}^{N}n^p \sim \frac{N^{p+1}}{p+1}$ has been asked and answered (through Riemann sums, Stolz-Cesàro, the hockey stick identity and simple inequalities) many times. — Jack D'Aurizio, Feb 13 '18 at 17:08
Does this answer your question? Prove that $\lim_{n\rightarrow\infty}\frac{1}{n^{p+1}}\sum_{k=1}^{n}k^{p}=\frac{1}{p+1} $ — Sil, Nov 22 '22 at 04:35

Guy Fsone · Answer 1 · 2018-02-14T04:49:19.407

1

By Riemann rectangle sum for $p>-1$ we have , $$ \lim_{n\to \infty}\frac{1}{n^{p+1}}\sum_{k=1}^{n}k^p \\= \lim_{n\to \infty}\frac{1}{n}\sum_{k=1}^{n}\left(\frac{k}{n}\right)^p\\=\int_0^1 x^p dx =\frac{1}{p+1}$$

That is also $$\lim_{n\to \infty}\left(\left(\frac{1}{n}\right)^p+\left(\frac{2}{n}\right)^p+\left(\frac{3}{n}\right)^p+...+1\right)\left(\frac{1}{n}\right)=\int_0^1x^pdx=\frac{1}{p+1} $$

edited Feb 14 '18 at 04:49

answered Feb 13 '18 at 16:59

Guy Fsone

23,903

Why $p<1?$ It's actually valid for $p>-1.$ It looks like you have things upside down here; the integral in question is $\int_0^1x^{p}, dx.$ – zhw. Feb 13 '18 at 23:46
Perhaps, strictly speaking, it is for $p \ge 0$. (See zhw solution.) The proof that Riemann sums converge to the Riemann integral requires first that it be Riemann integrable. Not merely improperly integrable, as with $\int x^p;dx, p<0$. There are examples of unbounded improperly integrable functions and Riemann sums that converge to the wrong thing. – GEdgar Feb 14 '18 at 12:35
@GEdgar I agreewith you but the OP did not specify any thing about the range of p. I just chose p so that the integral converges – Guy Fsone Feb 14 '18 at 13:47

score 1 · Answer 2 · answered Feb 13 '18 at 17:01

HINT

You can use that the function $\displaystyle x \mapsto \frac{1}{x^p}$ is continuous, positive and decreasing to $0$. We have the picture

Hence

$$ \int_{k}^{k+1}\frac{\text{d}t}{t^p} \leq \frac{1}{k^p} \leq \int_{k-1}^{k}\frac{\text{d}t}{t^p}$$

Hence using Chasles's relation $$ \int_{1}^{n}\frac{\text{d}t}{t^p} \leq \sum_{k=1}^{n}\frac{1}{k^p} \leq 1+\int_{1}^{n}\frac{\text{d}t}{t^p}$$

Can you take it from there ?

score 0 · Answer 3 · answered Feb 13 '18 at 23:43

You made a good start in your "idea". But you didn't recognize what you had. Let $p\ge 0, f(x) = x^p, x\in [0,1].$ Then what you wrote is

$$\tag 1 \sum_{k=1}^{n} f\left(\frac{k}{n}\right )\frac{1}{n}.$$

That should cause you to get excited. It's simply a standard Riemann sum for $f$ on $[0,1].$ Because $p\ge 0,$ $f$ is continuous on $[0,1],$ hence is Riemann integrable there. It follows that the limit of $(1)$ is

$$\int_0^1 f(x)\,dx = \int_0^1 x^p\,dx = \frac{x^{p+1}}{p+1}\big|_0^1 = \frac{1}{p+1}.$$

This result holds as well if we allow $-1<p<0,$ but it is more subtle. That's because $f$ is now unbounded, and we're dealing with improper (although convergent) integrals. If $p\le -1,$ a good exercise for you is to show the limit of those sums is $\infty.$

Proving $\lim \limits _{n\to \infty }\frac{1}{n^{p+1}}\sum\limits _{k=1}^{n \:}k^p=\frac{1}{p+1}$

3 Answers3