I'm looking for a specific limit of a function containing The lambert W function.
for the most simplified case, my function looks as follows:
$y=W(-rxe^x)$
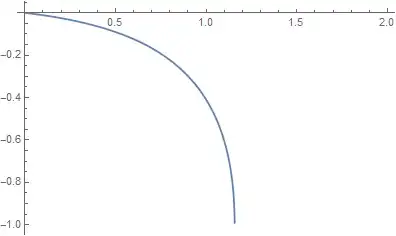
this is the plot of the function for $r=0.1$:
As you can see from the figure, $y\rightarrow -\infty$ somewhere $x\approx1.1$.
I would like to find this limit.
When I Inverse the function using mathematica, I get a solution (which I think is only one branch) of the form:
$x=W(-\frac{1}{r} y e^y)$
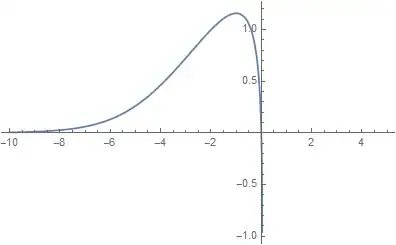
The mathematica plot of that function looks as follows:
As you can see from the figure, when $y\rightarrow\infty$, then $x\rightarrow0$.
This does not coincide with the previous result.
Can anyone please, reference, direct or explain how to solve the following problems:
Finding the inverse function of $y(x)=W(-rxe^x)$, i.e, $x(y)$.
Find the value of $x$ in which $y(x)=W(-rxe^x)$ converges to, in the limit of $y(x)\rightarrow -\infty$.