Projections of uniformly distributed $\mathbb{R}^3$ unit vector have uniform distribution

Question

My question revolves around the following property:

Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in \mathbb{R}^3$ $$X = {\bf u}^\mathrm{T} {\bf v}$$ has uniform distribution $$X \sim \mathcal{U}(-1,+1).$$

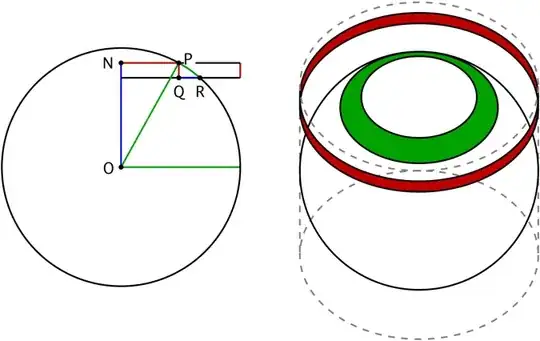
This can be proven easily by first arguing that $X$ has the same distribution as any canonical projection of $\bf u$ because of symmetry and then employing some geometry [which I did here under (12)]: for $x\in[-1,+1]$, write the CDF of $F_X(x)$ as the ratio of the surface areas between a cap of height $1+x$ of the unit sphere and the entire unit sphere. Quite surprisingly, the surface area of the cap is linear in its height $x$ and you get $$F_X(x) = \frac{2\pi(1+x)}{4\pi} = \frac{1+x}{2}$$ which is a uniform distribution on $[-1,+1]$ and finishes the proof.

My Problem: This seems like a very appealing property of three-dimensional space. It's so simple that certainly thousands of mathematicians have stumbled upon it. Yet I cannot find other sources or material on it. I use the property heavily in my work and I want as much info about it as possible, plus a strong mathematical source. I'm confident about my proof and of course I verified everything numerically, but I don't like being self-referential on such a basic thing.

My Question: Could you please provide me with the following?

• One or more good sources on the property.
• As much fruitful information and intuition about it as possible.

Thank you very much!

Appendix: Here's some more info that could ignite the discussion. For the same thing in $\mathbb{R}^1$ you get a discrete uniform distribution on $x \in \{-1,+1\}$. In $\mathbb{R}^2$ you get the PDF $f_X(x) = 1 /(\,\pi\sqrt{1-x^2}\,)$ with poles at $x = -1$ and $x = +1$. This shows: the lower the dimension, the more likely it is that $\bf u$ hits a direction similar to $\bf v$. For $\mathbb{R}^N$, the probabily mass of $f_X(x)$ becomes more and more concentrated near $0$ with increasing $N$ because high-dimensional random vectors tend to be orthogonal.

Answer 1

This was proved by Archimedes and has become known as "Archimedes' hat box theorem." They proved that if a sphere is inscribed in a vertical cylinder, the area of the sphere between two horizontal planes is the same as the area of the cylinder between those two planes; this is a reformulation of what you said. Archimedes gave two arguments: one in The Method of Mechanical Theorems based on his "law of the lever" physical reasoning, and one in On the Sphere and Cylinder by estimating the volume of sections of spherical shells, which he considered more rigorous. From a modern point of view it is a simple calculus exercise, see for example here.

Here are three generalizations you might find interesting:

• If $\mathbf x$ has the uniform distribution on the unit sphere in $\mathbb R^n,$ then $(x_1,\dots,x_{n-2})$ has the uniform distribution on the unit ball in $\mathbb R^{n-2}.$ The calculus proof is almost exactly the same. (This result has its own thread over on mathoverflow.)

• As mentioned by Greg Kuperberg on that thread, the height map $S^2\to [-1,1]$ is an example of the moment map of a toric symplectic manifold. For general toric symplectic manifolds there is a measure-preserving map to the "moment polytope" with the uniform distribution, the Duistermaat–Heckman measure.

• You can replace the vertical cylinder by a cone, and horizontal planes by spheres centred at the apex of the cone. See "A Generalisation of Archimedes' Hatbox Theorem" by De Silva, http://www.jstor.org/stable/3621436

Answer 2

This property is an immediate consequence of the fact that the "horizontal projection" of $S^2$ onto a cylinder of height $2$ enveloping $S^2$ along the equator is rotationally symmetric with respect to the $z$-axis and area preserving.

Answer 3

Hint:

In this answer it is shown that the area of the green region on the sphere is the same as the area of the red region on the cylinder. The area of the red region on the cylinder is $2\pi$ times the radius of the cylinder times the length of the projection of the green or red region onto the axis of the cylinder.