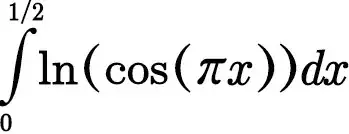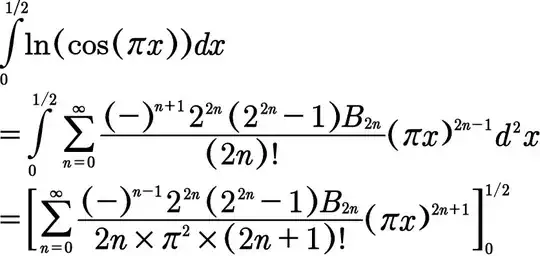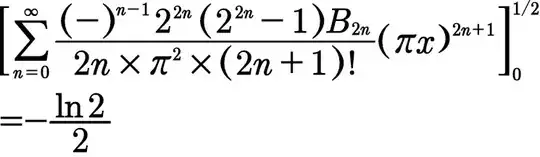Asked
Active
Viewed 79 times
-1
-
3This isn't a physics question. – Chris Feb 09 '18 at 05:56
-
We'd prefer you use Mathjax for equations, not images. It's the site standard. – StephenG - Help Ukraine Feb 09 '18 at 06:29
-
What is $d^2 x$? See http://math.stackexchange.com/questions/341643/showing-that-int-01-log-sin-pi-xdx-log2 and http://math.stackexchange.com/questions/333941/how-to-computer-int-01-log-sin-pi-x-textdx-under-complex-methods – FDP Feb 09 '18 at 11:43
1 Answers
1
Let $I=\int_0^{1/2}\ln\cos\pi x dx=\pi^{-1}\int_0^{\pi/2}\ln\cos y dy$ so $I=\pi^{-1}\int_0^{\pi/2}\ln\sin y dy$ and $$2\pi I =\int_0^{\pi/2}\ln(\sin y\cos y) dy=\int_0^{\pi/2}\ln\sin 2y dy-\frac{\pi }{2}\ln 2=\frac{1}{2}\int_0^{\pi}\ln\sin x dx-\frac{\pi }{2}\ln 2.$$ Hence $$2\pi I=\int_0^{\pi/2}\ln\sin x dx-\frac{\pi }{2}\ln 2=\pi I -\frac{\pi }{2}\ln 2,$$ giving $I=-\frac{1}{2}\ln 2$ as you obtained.
J.G.
- 115,835