5

There are n points located arbitrarily on the plane. Let us perform the following transformation: every point 'jumps' to the nearest one. 'A jumps to B' means that the point A coordinates after the transformation are equal to the coordinates of the point B before the transformation. If there are several points (B and C) with the same minimal distance from A (AB = AC), it can jump to any of them (A to B or A to C), so you can choose favorable option. If some points have equal coordinates after the transformation they merge to one point, effectively reducing the number of remaining points. All the jumps happen simultaneously (there are only two states of the system). What is the minimum number of points after the transformation?

Some examples:

1) 2 points A and B. The only thing that can happen is that A jumps to B and B jumps to A. Essentially, they just swap places.

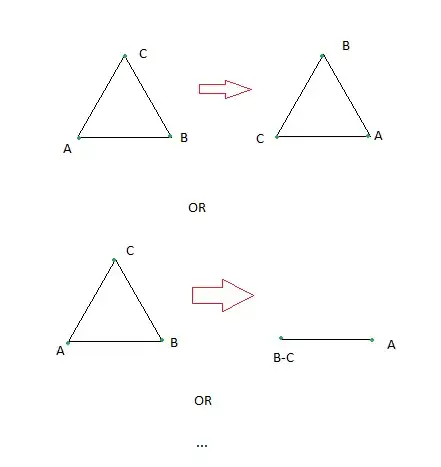
2) Three points A, B, C at the vertices of an equilateral triangle. Every point can jump to one of the others. For instance, A to B, B to C, C to A (three-way swap) or A to B, B to A, C to A (B and C have merged, there are only 2 points now: B-C and A) or etc. The second option is better and, since we are looking for the minimum number of remaining points, for n=3 the answer is 2.

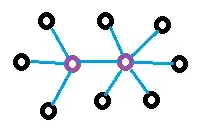
enter image description here

I was thinking about the solution with small n. It seems obvious that seven points should be arranged in the center and vertices of a hexagon. 7 points to 2 is a good ratio. Two hexagons with a common vertex produces (for 13 points) the better ratio (13 to 3), if 2 central points from the adjacent hexagons jump to the same place.

I am almost sure that there is a better way of arranging points on the plane, but currently I am out of ideas. Do you have any suggestions?

Ego
  • 53
  • 1
    Welcome to stackexchange. I think your question is potentially interesting, but unclear. I don't understand "jumping", or choosing points at random, or "points left". Are you just looking for an arrangement with a high fraction of the minimum distances equal to $1$? Please edit the question to clarify (don't answer in a comment). – Ethan Bolker Feb 06 '18 at 13:30
  • It's clearer now but still not clear. How do you decide if $A$ jumps to $B$ or $B$ to $A$? Do the jumps happen simultaneously or in random or alphabetical order? What if there are three at the vertices of an equilateral triangle? If you edit the question to show a few small cases explicitly, maybe with pictures, perhaps we can help. – Ethan Bolker Feb 06 '18 at 15:00

1 Answers1

2

You can arrange up to 10 points in this way:

enter image description here

Where they are all in a hexagonal grid, so that the black points map to one of the the purple points and the purple points each map to the other.

Another three points can be added while only increasing the final count by one:

enter image description here

where each of the new points goes to the same black point.

These two shapes can be repeated any number of times without interfering with eachother, so the answer to the problem is:

$$\text{minimum}(n) = \begin{cases} \text{if }n > 10\land(n\text{ mod }10) \in \{1, 2, 3\}: & 2\left\lceil\frac{n}{10}\right\rceil-1\\ \text{else:} & 2\left\lceil\frac{n}{10}\right\rceil \end{cases}$$

Because we can have $\left\lceil\frac{n}{10}\right\rceil$ clusters of ten, each consuming ten points and resulting in two, and we can add up to three additional points to one of those clusters while only adding a single extra point.

Proof that this is the optimal way relies on the fact that at most six points can map to a single one, and any point mapping to a "full" point can only have at most three new points mapped to it.

Austin Weaver
  • 2,059