I have no idea how this equation: \begin{equation} (x^2 + y^2 - 1)^3 - x^2 y^3 = 0 \end{equation}
Produces this picture:
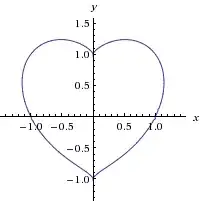
Can someone provide a general explanation of plotting this function?
I have no idea how this equation: \begin{equation} (x^2 + y^2 - 1)^3 - x^2 y^3 = 0 \end{equation}
Produces this picture:

Can someone provide a general explanation of plotting this function?
The solution set is obviously symmetric with respect to the $y$-axis. Therefore we may assume $x\geq 0$. In the domain $\{(x,y)\in {\mathbb R}^2\ |\ x\geq0\}$ the equation is equivalent with $$x^2+ y^2 -1=x^{2/3} y\ ,$$ which can easily be solved for $y$: $$y={1\over2}\bigl(x^{2/3}\pm\sqrt{x^{4/3}+4(1-x^2)}\bigr)\ .$$ Now plot this, taking both branches of the square root into account. You might have to numerically solve the equation $x^{4/3}+4(1-x^2)=0$ in order to get the exact $x$-interval.
It's easier to be understood in polar coordinates.
(x^2 + y^2 - 1)^3 - x^2*y^3 == 0 /. {x -> r*Cos[\[Theta]],
y -> r*Sin[\[Theta]]} // FullSimplify
% // ApplySides[#/r^5 &, #] &
$$ \left(r^2-1\right)^3=r^5 \sin ^3(\theta ) \cos ^2(\theta ) \\ \frac{\left(r^2-1\right)^3}{r^5}=\sin ^3(\theta ) \cos ^2(\theta ) $$
Plot[Sin[\[Theta]]^3*Cos[\[Theta]]^2, {\[Theta], 0, 2 Pi}]
Plot[(r^2 - 1)^3/r^5, {r, 0, 5}]
Starting from @Christian Blatter's solution $$x^{\frac 43}+4(1-x^2)=0$$
$$x=t^{\frac 32} \qquad \implies \qquad 4 t^3-t^2-4=0$$
$$t=\frac{1}{12} \left(1+2 \cosh \left(\frac{1}{3} \cosh ^{-1}(865)\right)\right)$$ When $a$ is large $$ \cosh^{-1}(a)=(\log (a)+\log (2))-\frac{1}{4 a^2}-\frac{3}{32 a^4}+O\left(\frac{1}{a^6}\right)$$ So
$$t\sim \frac{1}{12} \left(1+\sqrt[3]{2a}+\frac{1}{\sqrt[3]{2a}}\right)\qquad \text{where} \qquad a=865$$ which is in a absolute error of $1.106\times 10^{-7}$.