0

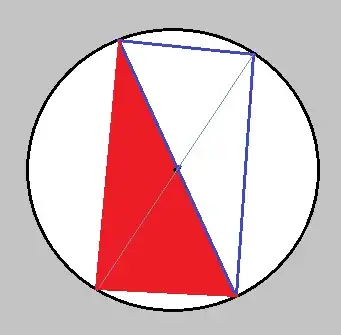
At first, we pick a random point.

Then there are infinite number of options for our next pick and only one point that is diagonally opposite to our first pick.

Therefore, the probability is $\frac 1\infty = 0$.

Does that mean that there is no chance or that it is infinitely small? If we are solving any probability problem, do we completely disregard these cases since there is (practically) no chance of them occurring?

PS: Why am I asking?

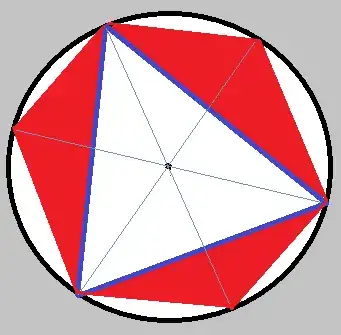
I stumbled upon a problem asking to find the probability that the centre of a circle is contained in the triangle formed by three randomly selected points on it. I now know how to solve it, but I approached it in a different way initially. Namely:

I found that for any triangle that contains the centre there exist three 'outer' triangles formed by the diagonal projection of each of its vertices. These sets of 4 triangles are uniquely determined by any one of them. 1 of them always contains the centre and 3 of them don't. Therefore, the probability sought must be $\frac14$. This is actually the correct answer.

Figure 1

What bugs me are the special cases when the centre lies on one of the sides of the triangles. Then there are 2 uniquely determined triangles both of which contain the centre. If the probability of selecting two points that lie on the same diagonal is $0$, then it would be fine. But I have the feeling I am missing something.

Figure 2

Rayhunter
  • 837

2 Answers2

2

Do not disregard them. They have probability $0$ but they may happen. For a more intuitive and simpler example of this phenomenon: consider $X$, a uniformly distributed random variable on $[0,1]$. What is the probability that $X = \frac{1}{2}$? Answer: it's $0$. But what is the probability of $\cup_{x \in [0,1]} (X = x)$? That's $1$.

If you keep thinking of it in your current terms, all those little nothings add up to a $1$, and that way madness lies. Just remember that something can happen even though its probability is $0$.

Patrick Stevens
  • 36,135
0

It means the chances are ... $0$. It is just the same thing when you toss infinitely a fair coin (you can imagine that each toss gives you a digit of your number (the point you peak next can be represented as a number : the distance on the circle from the first point chosen) in base 2) : it is not impossible to have only "tails", but it is a $0$ probability event...

Netchaiev
  • 4,811