2

I'm searching for a nice mean (or average) for negative numbers that gives less weight to high (absolut) outliers (I don't have enough values to use median). Obviously the way to go for positive values is the geometric mean but this is not working (without transformation) for negative values. To be more precise I a series with negative and positive values ranging from $[-1, 1]$.

Looking for some alternatives I found:

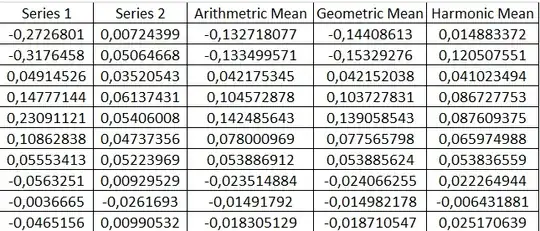
Using these methods and comparing them to the arithmetic mean I get:

enter image description here

Both the harmonic Mean and the geometric mean are larger than the arithmetic mean (in absolute terms). Is there another method I can use or do I make a mistake?

Thank you.

p.s. I was looking at the geometric mean again and I used $x=100000$ instead of $x=1$ and now my results for the geometric mean are very close to the arithmetic which is mentioned in the link above. So this method is not really a workaround but a dilluted method for the arithmetic mean.

Community
  • 1
PAS
  • 147
  • If you don’t have enough values to use a median then how can you even say what an outlier looks like? E.g if you get $(0.9,0.1)$ which is the outlier? Maybe what you want to do is put all your data through some function ($1/x$ maybe?) and take means (and maybe take them back). You won’t be able to put much meaning to anything you do if you are only ever trying to average two things. – Dan Robertson Feb 01 '18 at 14:05
  • Good point and you are totally right. The term "outlier" is wrong or at least misleading. (But maybe one could think about the above series as two different time series for financial data with an outlier as a "jump" from one time t to time t+1. ) Nevertheless you are also correct with your statement about the "meaning" of the average of only two things but there are no additional series available. I will try your suggestion with $1/x$. – PAS Feb 01 '18 at 14:15
  • If you care about time series then this is the wrong way to analyse these. – Dan Robertson Feb 01 '18 at 14:16
  • I don't want to go too much into detail (not the reason for this question) but the basic idea is to compare different parts of a time series around a certain event which is pretty common in economics, for example the development of a time series around a recession. Series 1 and Series 2 are just different parts of the same time series. – PAS Feb 01 '18 at 14:41

0 Answers0