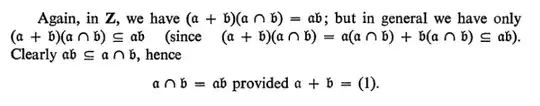For $I,J$ ideals, show that $IJ\subseteq (I\cap J)(I+J)$. If it helps $I$ and $J$ are ideals in a Dedekind domain, but as far as I can tell the proof given in the book only uses the fact that we are in a commutative ring, either way I can't follow the proof:
If $ab\in IJ$ for $a\in I$ and $b\in J$, then $ab\in I,J$ and thus $ab\in I\cap J$. Furthermore we can see that $ab\in I+J$. Therefore $ab\in (I\cap J)(I+J)$.
Everything is rather straightforward up to the 'therefore' at the end. Just because something is in two ideals doesn't mean it's in their product, so we know that $(ab)^2\in (I\cap J)(I+J)$, but I can't see how it follows that $ab\in (I\cap J)(I+J)$. Thanks
This is Lemma 1.3 from page 30 of Mollin's Algebraic Number Theory.