Find a combinatorial proof for $\binom{n+1}{k} = \binom{n}{k} + \binom{n-1}{k-1} + ... + \binom{n-k}{0}$

Question

Let $n$ and $k$ be integers with $n \geq k \geq 0$. Find a combinatorial proof for

$$\binom{n+1}{k} = \binom{n}{k} + \binom{n-1}{k-1} + \cdots + \binom{n-k}{0} .$$

My approach: I was thinking to use the binomial formula as in $$2^n = \sum{\binom{n}{k}1^k1^{n-k}} .$$ I also tried to use Pascal's Identity $\binom{n}{r}=\binom{n-1}{r-1}+\binom{n-1}{r}$.

Answer 1

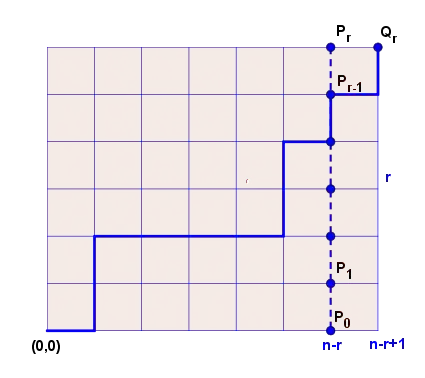
I think you can try to interpret this identity using the following real-life problem:

Imagine you have a plate of $n+1$ treats: $k$ of them are chocolate pieces, and the rest are Brussels sprouts. In how many ways can you eat all of them, one by one? Assume the chocolate pieces are indistinguishable from each other, and so are Brussels sprouts.

The answer is, of course, $\binom{n+1}{k}$. However, let's count differently, depending on what you eat first:

• You bravely go straight on to a Brussels sprout, before eating any chocolate. There are $\binom{n}{k}$ ways to do that, as there will be $n$ treats left and $k$ of them are chocolate pieces;
• You first eat one piece of chocolate, and then go on to eating a Brussels sprout: there are $\binom{n-1}{k-1}$ ways to do that, as there will be $n-1$ treats left, $k-1$ of them chocolate;
• You first eat two pieces of chocolate, then go on to a Brussels sprout: similarly, it can be done in $\binom{n-2}{k-2}$ ways;
• You first eat three pieces of chocolate...

etc. until:

• You eat $k-1$ chocolate pieces first, then one Brussels sprout. Then, only one of the remaining $n-(k-1)$ treats is a chocolate, and the number of ways to do that is $\binom{n-(k-1)}{1}$;
• You eat all the chocolate pieces first, and then you eat all of the Brussels sprouts: it can be done in only one way, which can also be written as $1=\binom{n-k}{0}$.

Generally, if you eat first $m$ pieces of chocolate ($0\le m \le k$) before getting on with your first Brussels sprout, there are $\binom{n-m}{k-m}$ ways to do it: after eating the initial chocolate pieces and the Brussels sprout, there will be $n-m$ treats left on the plate, $k-m$ of them being chocolate, so you can eat them in $\binom{n-m}{k-m}$ ways.

Altogether all those numbers must add to our original result $\binom{n+1}{k}$, i.e.

$$\binom{n+1}{k}=\binom{n}{k}+\binom{n-1}{k-1}+\binom{n-2}{k-2}+\cdots+\binom{n-(k-1)}{1}+\binom{n-k}{0}=\sum_{m=0}^k\binom{n-m}{k-m}$$

Answer 2

It follows from Pascal's identity that\begin{align}\binom{n+1}k&=\binom nk+\binom n{k-1}\\&=\binom nk+\binom{n-1}{k-1}+\binom{n-1}{k-2}\\&=\binom nk+\binom{n-1}{k-1}+\binom{n-2}{k-2}+\binom{n-2}{k-3}\\&=\cdots\end{align}Can you take it from here?

Answer 3

A combinatorial proof based upon lattice paths.

The number of lattice paths of length $n+1$ from $(0,0)$ to $Q_k=(n-k+1,k)$ consisting of $(1,0)$-steps and $(0,1)$-steps is $$\binom{n+1}{n-k+1}=\binom{n+1}{k}$$ since we have to choose precisely $n-k+1$ $(1,0)$-steps from a total of $n+1$ steps.

                                

We observe that each path which goes from $(0,0)$ to $Q_k$ crosses the vertical line $x=n-k$. We can therefore partition all $\binom{n+1}{k}$ paths according to points $P_j=(n-k,j), 0\leq j\leq k$ which are followed by a horizontal step to $(n-k+1,j)$ and the vertical steps which lead to $Q_k$.

Since there are precisely $\binom{n-k+j}{j}$ paths from $(0,0)$ to $P_j$ the number of all paths from $(0,0)$ to $Q_r=(n-k+1,k)$ is \begin{align*} \color{blue}{\binom{n+1}{k}=\binom{n}{k}+\binom{n-1}{k-1}+\cdots+\binom{n-k}{0}} \end{align*}

Answer 4

From Pascal's triangle we see that the sum is equivalent to

$$\sum_{i=n-k}^n\binom{i}{n-k}$$

then refer to Hockey-stick identity

$$\sum^m_{i=s}{i\choose s}={m+1\choose s+1} \qquad \text{ for } m,s\in\mathbb{N}, \quad m>s$$